Mutant Modes

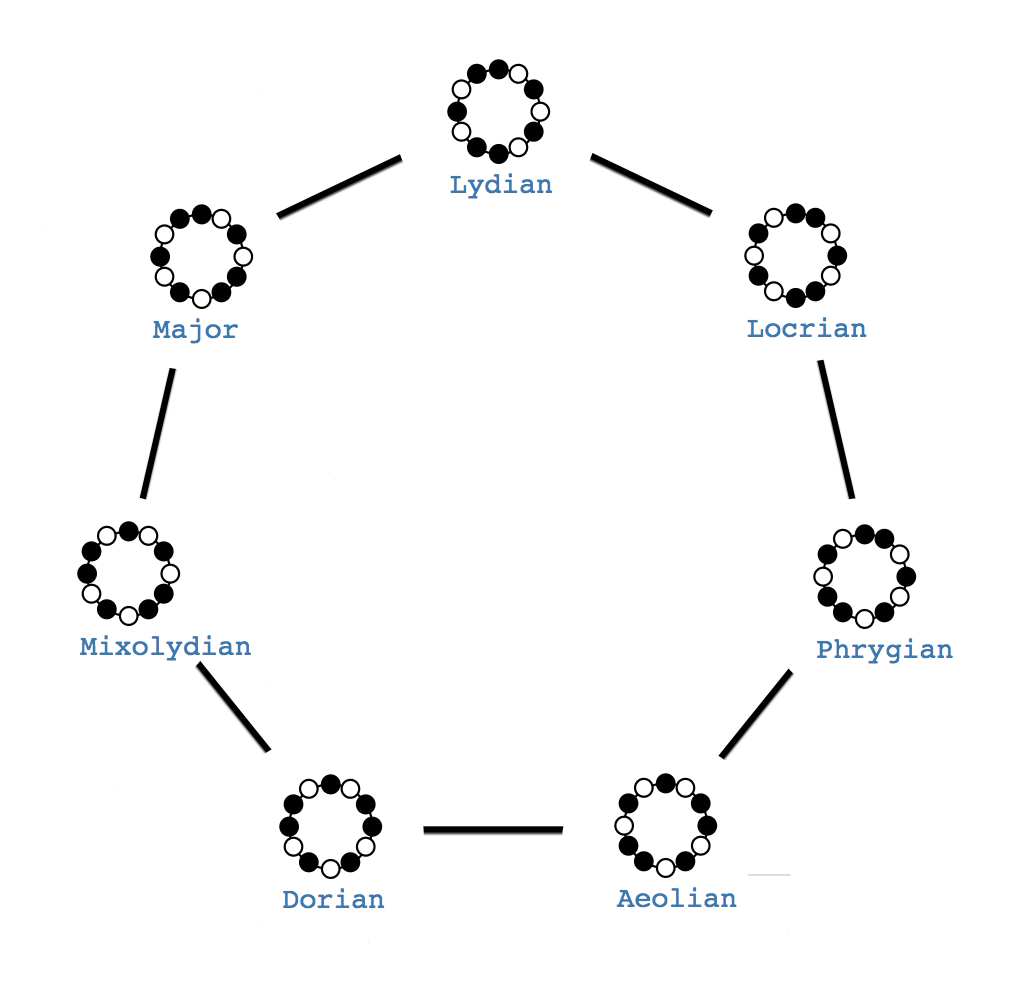
There is a pattern of mutation connecting all the diatonic modes (rotations of the major scale). They proceed in this order:

Lydian Major Mixolydian Dorian Aeolian Phrygian Locrian

Scale 2773		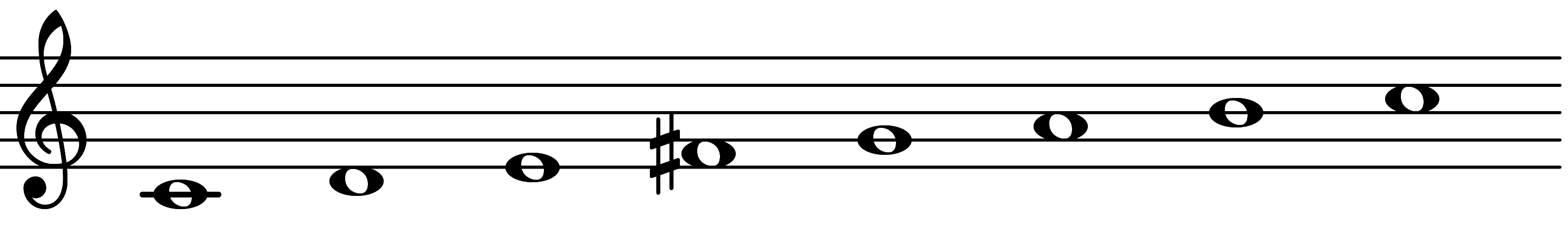		Lydian
Scale 2741				Major
Scale 1717				Mixolydian
Scale 1709				Dorian
Scale 1453				Natural Minor
Scale 1451				Phrygian
Scale 1387				Locrian

Starting at the Lydian, if we lower the 4th degree, we get the Major (Ionian) scale.
When we lower the 7th degree of the Major scale, we get the Mixolydian scale.
When we lower the 3th degree of the Mixolydian scale, we get the Dorian scale.
When we lower the 6th degree of the Dorian scale, we get the Aeolian scale.
When we lower the 2nd degree of the Aeolian scale, we get the Phrygian scale.
When we lower the 5th degree of the Phrygian scale, we get the Locrian scale.

From the C Locrian pictured above, if we lower the 1st step, we arrive at C flat Lydian! The cycle repeats all over, rooted a semitone lower.

That's pretty cool, isn't it? Every mode of the scale is related to two others by mutation, and every other by rotation.

This seems like a peculiar quality, and I was led to ask: Do any other scales fit together this way?

A convenient fact is that if a scale has this property, then we'll see that from one end of the chain (eg. Lydian) there is a mode with a Levenshtein Distance of 1, another mode with a distance of 2, and so on up to the nth mode with a distance of n, where n is one less than the number of tones in the scale. The same pattern will exist starting from the other end of the chain (e.g. Locrian).

Even though our distance algorithm measures the distance between Locrian and Lydian is 6, we could argue that the true distance is 1 if we allow a mutable root. With a mutable root distance algorithm, calculating the distance between scales would uncover many more nearby scales than the one we have used for finding Mutant Modes.

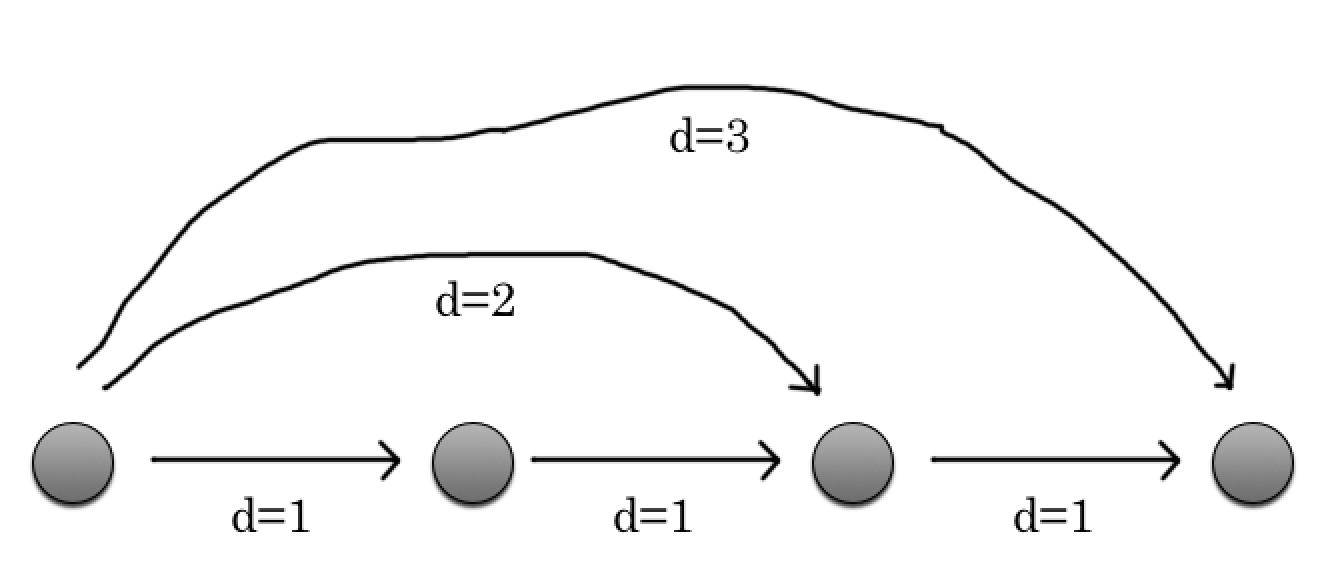
Thanks to this fact, we don't need to calculate the distance between steps for every permutation of modes, searching for one with a pattern of [1,1,1,1,1...]. That would be an incredibly intensive and expensive calculation. Instead we can loop though all the scales, finding any that have distances to its modes matching [0,1,2,3,...,n].

function isMutant($scale) {
	$modes = $scale->modes();
	if (count($modes) == 1) {
		return false;
	}
	$dists = getDistances($scale);
	for ($i=0; $i<count($modes); $i++) {
		if (!in_array($i, $dists)) {
			return false;
		}
	}
	return true;
}

function getDistances($scale) {
	$modes = $scale->modes();
	$middleC = new \ianring\Pitch('C', 0, 4);
	$distances = array();
	foreach($modes as $index=>$mode) {
		$modeScale = new \ianring\Scale($mode, $middleC);
		$dist = \ianring\Scale::levenshteinScale($scale->scale, $mode);
		$distances[$mode] = $dist;
	}
	return $distances;
}

Result

When we crunch the numbers, we find there are only 4 scales that satisfy the criteria. They are:

Scale 661				Major Pentatonic
Scale 1321		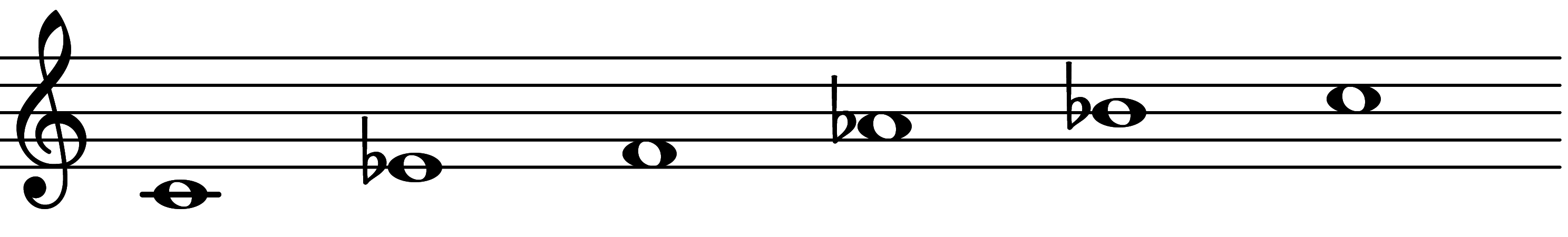		Rāga Malakosh
Scale 1387				Locrian
Scale 2773		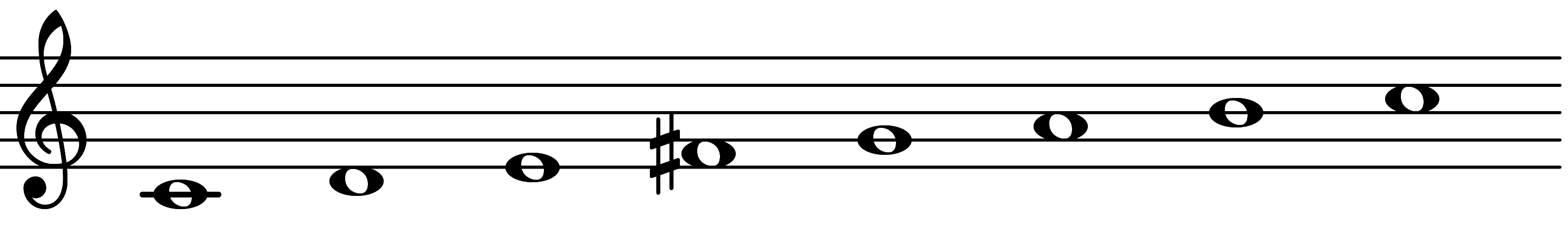		Lydian

Thus we find there are only two modal families that have this pattern of mutation!

They are the major diatonic scale and all its modes:

Lydian Major Mixolydian Dorian Aeolian Phrygian Locrian

...and its complement, the major pentatonic, and its modes:

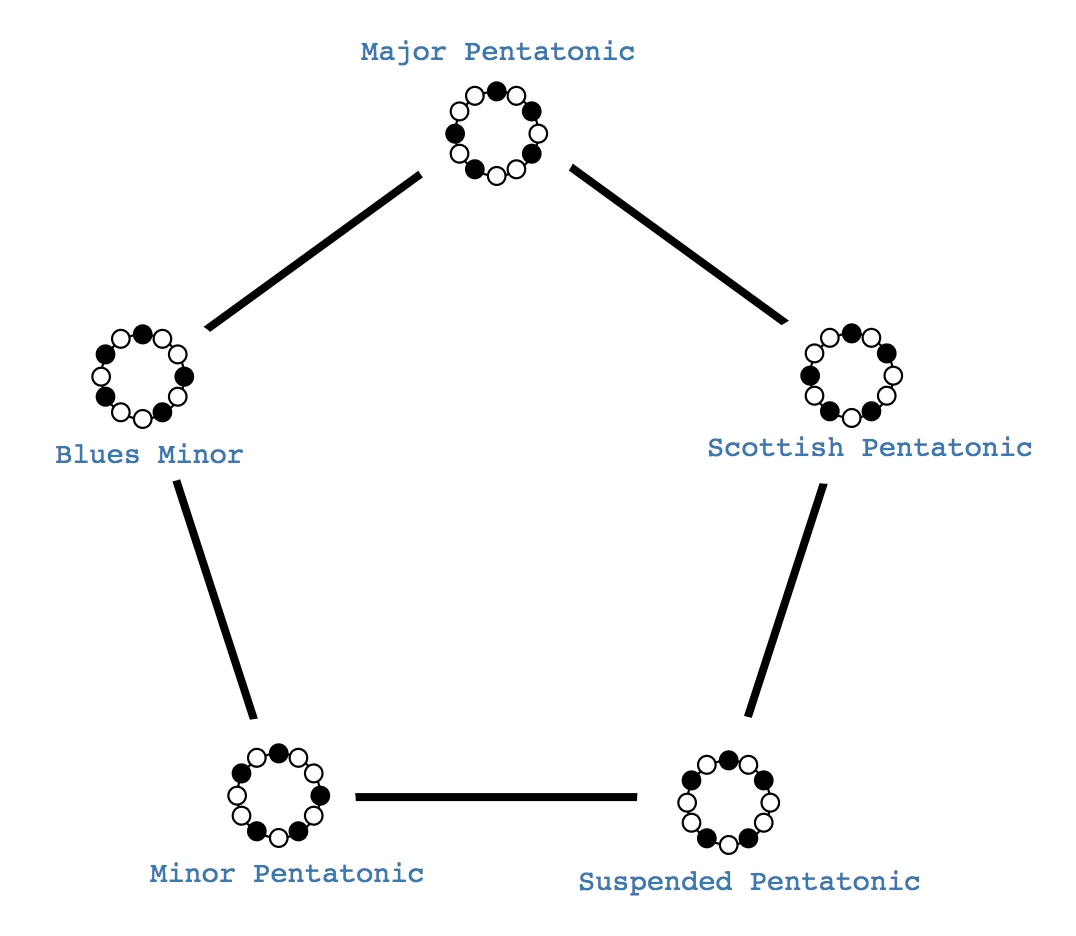
Major Pentatonic Scottish Pentatonic Suspended Pentatonic Minor Pentatonic Blues Minor

It's not coincidence that these two modal families are complements of each other, and they are the maximally even sets for the only two cardinalities that are coprime with 12.

Addendum

Years after this essay was originally written, I became aware that this notion of "mutant modes" was very closely related - if not identical - to the concept of "Deep Scales" as described by Terry Winograd in an unpublished paper back in 1966. I have acquired a copy of this paper directly from the author, where the mathematical properties of this sort of transformation are explored in fascinating detail. There will be a chapter about Deep Scales in the book.