The Exciting Universe Of Music Theory
presents

Myhill's Property

Myhill's property was discovered and named by John Clough and Gerald Myerson, who had been exploring the patterns known as CV (Cardinality Equals Variety) and SM (Structure Yeilds Multiplicity) in well-formed sets. They observed and proved that when CV is true, every interval has a two-element spectrum. John Myhill contributed the conjecture that the reverse was also true, and the two properties were synonymous, and brought Clough and Myerson together to work on the problem. Subsequently they named the property after their mathematical mentor.

PrimeOther transformationsSpectrum
2-1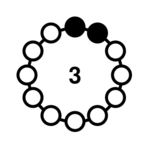6, 12, 24, 48, 96, 192, 384, 768, 1536, 2049, 3072
<1> = {1, 11}
2-2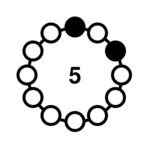10, 20, 40, 80, 160, 320, 640, 1025, 1280, 2050, 2560
<1> = {2, 10}
2-3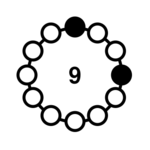18, 36, 72, 144, 288, 513, 576, 1026, 1152, 2052, 2304
<1> = {3, 9}
2-434, 68, 136, 257, 272, 514, 544, 1028, 1088, 2056, 2176
<1> = {4, 8}
2-566, 129, 132, 258, 264, 516, 528, 1032, 1056, 2064, 2112
<1> = {5, 7}
3-1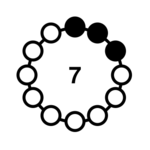14, 28, 56, 112, 224, 448, 896, 1792, 2051, 3073, 3584
<1> = {1, 10}
<2> = {2, 11}
3-6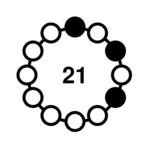42, 84, 168, 336, 672, 1029, 1281, 1344, 2058, 2562, 2688
<1> = {2, 8}
<2> = {4, 10}
3-9161, 266, 322, 532, 644, 1057, 1064, 1288, 2114, 2128, 2576
<1> = {2, 5}
<2> = {7, 10}
3-10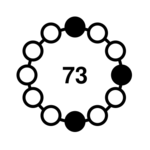146, 292, 521, 577, 584, 1042, 1154, 1168, 2084, 2308, 2336
<1> = {3, 6}
<2> = {6, 9}
4-1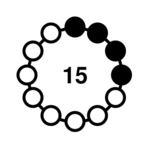30, 60, 120, 240, 480, 960, 1920, 2055, 3075, 3585, 3840
<1> = {1, 9}
<2> = {2, 10}
<3> = {3, 11}
4-21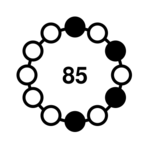170, 340, 680, 1045, 1285, 1345, 1360, 2090, 2570, 2690, 2720
<1> = {2, 6}
<2> = {4, 8}
<3> = {6, 10}
5-1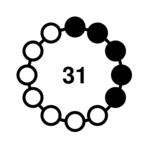62, 124, 248, 496, 992, 1984, 2063, 3079, 3587, 3841, 3968
<1> = {1, 8}
<2> = {2, 9}
<3> = {3, 10}
<4> = {4, 11}
5-33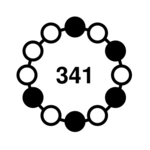682, 1109, 1301, 1349, 1361, 1364, 2218, 2602, 2698, 2722, 2728
<1> = {2, 4}
<2> = {4, 6}
<3> = {6, 8}
<4> = {8, 10}
5-35677, 1189, 1193, 1321, 1322, 1354, 2378, 2386, 2642, 2644, 2708
<1> = {2, 3}
<2> = {4, 5}
<3> = {7, 8}
<4> = {9, 10}
6-1126, 252, 504, 1008, 2016, 2079, 3087, 3591, 3843, 3969, 4032
<1> = {1, 7}
<2> = {2, 8}
<3> = {3, 9}
<4> = {4, 10}
<5> = {5, 11}
7-1254, 508, 1016, 2032, 2111, 3103, 3599, 3847, 3971, 4033, 4064
<1> = {1, 6}
<2> = {2, 7}
<3> = {3, 8}
<4> = {4, 9}
<5> = {5, 10}
<6> = {6, 11}
7-351451, 1453, 1709, 1717, 2741, 2773, 2774, 2902, 2906, 3418, 3434
<1> = {1, 2}
<2> = {3, 4}
<3> = {5, 6}
<4> = {6, 7}
<5> = {8, 9}
<6> = {10, 11}
8-1510, 1020, 2040, 2175, 3135, 3615, 3855, 3975, 4035, 4065, 4080
<1> = {1, 5}
<2> = {2, 6}
<3> = {3, 7}
<4> = {4, 8}
<5> = {5, 9}
<6> = {6, 10}
<7> = {7, 11}
9-1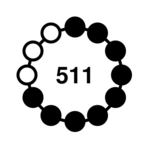1022, 2044, 2303, 3199, 3647, 3871, 3983, 4039, 4067, 4081, 4088
<1> = {1, 4}
<2> = {2, 5}
<3> = {3, 6}
<4> = {4, 7}
<5> = {5, 8}
<6> = {6, 9}
<7> = {7, 10}
<8> = {8, 11}
10-12046, 2559, 3327, 3711, 3903, 3999, 4047, 4071, 4083, 4089, 4092
<1> = {1, 3}
<2> = {2, 4}
<3> = {3, 5}
<4> = {4, 6}
<5> = {5, 7}
<6> = {6, 8}
<7> = {7, 9}
<8> = {8, 10}
<9> = {9, 11}
11-13071, 3583, 3839, 3967, 4031, 4063, 4079, 4087, 4091, 4093, 4094
<1> = {1, 2}
<2> = {2, 3}
<3> = {3, 4}
<4> = {4, 5}
<5> = {5, 6}
<6> = {6, 7}
<7> = {7, 8}
<8> = {8, 9}
<9> = {9, 10}
<10> = {10, 11}

Citations