A Study of Scales
Where we discuss every possible combination of notes
PREFACE. This essay was written in 2009. Since then, a few errata have been corrected and I embedded the youtube videos, but there have been no substantial additions. I think it still holds up fairly well, but if I were to rewrite it today, I would change some things. My main regret is using the criteria of maximum interval size throughout, since it skews some of the scale metrics and obscures symmetries and patterns we can find in the whole set of pitch class sets.
This essay barely scratches the surface of the rich theoretical work around scale properties. If you are itching for a more comprehensive tome, you're in luck: I'm writing a BOOK.
Assumptions
This exploration of scales is based in a musical universe founded on two assumptions:
-
Octave Equivalence
We assume that for the purpose of defining a scale, a pitch is functionally equivalent to another pitch separated by an octave. So it follows that if you're playing a scale in one octave, if you continue the pattern into the next octave you will play pitches with the same name. -
12 tone equal temperament
We're using the 12 tones of an equally-tempered tuning system, as you'd find on a piano. Equal temperament asserts that the perceptual (or functional) relationship between two pitches is the same as the relationship between two other pitches with the same chromatic interval distance. Other tuning systems have the notion of scales, but they're not being considered in this study.
Representing a scale
When I began piano lessons as a child, I learned that a scale was made up of whole- and half-steps. The scale was essentially a stack of intervals piled up, that happened to add up to an octave. While this view of the scale is useful for understanding diatonic melodies, it's not a convenient paradigm for analysis. Instead, we should regard a scale as being a set of 12 possibilities, and each one is either on or off.
Here is the major scale, in lights.












What we have in the 12-tone system is a binary "word" made of 12 bits. We can assign one bit to each degree of the chromatic scale, and use the power of binary arithmetic and logic to do some pretty awesome analysis with them. When represented as bits it reads from right to left - the lowest bit is the root, and each bit going from right to left ascends by one semitone.
The total number of possible combinations of on and off bits is called the "power set". The number of sets in a power set of size n is (2^n). Using a word of 12 bits, the power set (2^12) is equal to 4096. The fun thing about binary power sets is that we can produce every possible combination, by merely invoking the integers from 0 (no tones) to 4095 (all 12 tones).
This means that every possible combination of tones in the 12-tone set can be represented by a number between 0 and 4095. We don't need to remember the fancy names like "phrygian", we can just call it scale number 1451. Convenient!
| decimal | binary | |
|---|---|---|
| 0 | 000000000000 | no notes in the scale |
| 1 | 000000000001 | just the root tone |
| 1365 | 010101010101 | whole tone scale |
| 2741 | 101010110101 | major scale |
| 4095 | 111111111111 | chromatic scale |
An important concept here is that any set of tones can be represented by a number. This number is not "ordinal" - it's not merely describing the position of the set in an indexed scheme; it's also not "cardinal" because it's not describing an amount of something. This is a nominal number because the number *is* the scale. You can do binary arithmetic with it, and you are adding and subtracting scales with no need to convert the scale into some other representation.
Because scales are cyclical - they repeat and continue beyond a single octave - it is intuitive to represent them in "bracelet" notation. This visual representation is useful because it helps conceptualize modes and rotation (which we'll get into further below).
Here is the major scale, represented as a bracelet. Black beads are on bits, white beads are off bits.
If you imagine the bracelet with clock numbers, the topmost bead - at 12 o'clock - is the root, or 1st degree of the scale. Beware that in some of the math, this is the "0" position, as if we're counting semitones above the root. To play a scale ascending, start from the top and move around it clockwise. To play the scale descending, start at 12 o'clock and go around counterclockwise.
Interval Pattern
Another popular way of representing a scale is by its interval pattern. When I was learning the major scale, I was taught to say aloud: "tone, tone, semitone, tone, tone, tone, semitone". Many music theorists like to represent a scale this way because it's accurate and easy to understand: "TTSTTTS". Having a scale's interval pattern has merit as an intermediary step can make some kinds of analysis simpler. Expressed numerically - which is more convenient for computation - the major scale is [2,2,1,2,2,2,1].
Pitch Class Sets
Yet another way to represent a scale is as a "pitch class set", where the tones are assigned numbers 0 to 11 (sometimes using "T" and "E" for 10 and 11), and the set enumerates the ones present in the scale. A pitch class set for the major scale is notated like this: {0,2,4,5,7,9,11}. The "scales" we'll study here are a subset of Pitch Classes (ie those that have a root, and obey Zeitler's Rules1) and we can use many of the same mathematical tricks to manipulate them.
What is a scale?
Or more importantly, what is *not* a scale?
Now that we have the superset of all possible sets of tones, we can whittle it down to exclude ones that we don't consider to be a legitimate "scale". We can do this with just two rules.
-
A scale starts on the root tone.
This means any set of notes that doesn't have that first bit turned on is not eligible to be called a scale. This cuts our power set in exactly half, leaving 2048 sets.
In binary, it's easy to see that the first bit is on or off. In decimal, you can easily tell this by whether the number is odd or even. All even numbers have the first bit off; therefore all scales are represented by an odd number.
We could have cut some corners in our discussion of scales by omitting the root tone (always assumed to be on) to work with 11 bits instead of 12, but there are compelling reasons for keeping the 12-bit number for our scales, such as simplifying the analysis of symmetry, simplifying the calculation of modes, and performing analysis of sonorities that do not include the root, where an even number is appropriate.
scales remaining: 2048
-
A scale does not have any leaps greater than n semitones.
For the purposes of this exercise we are saying n = 4, a.k.a. a major third. Any collection of tones that has an interval greater than a major third is not considered a "scale". This configuration is consistent with Zeitler's constant used to generate his comprehensive list of scales.
scales remaining: 1490
Now that we've whittled our set of tones to only the ones we'd call a "scale", let's count how many there are with each number of tones.
| number of tones | how many scales |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 1 |
| 4 | 31 |
| 5 | 155 |
| 6 | 336 |
| 7 | 413 |
| 8 | 322 |
| 9 | 165 |
| 10 | 55 |
| 11 | 11 |
| 12 | 1 |
Modes
There is a lot of confusion about what is a "mode", chiefly because the word is used slightly differently in various contexts.
When we say "C major", the word "major" refers to a specific pattern of whole- and half-steps. The "C" tells us to begin that pattern on the root tone of "C".
Modes are created when you use the same patterns of whole- and half-steps, but you begin on a different step. For instance, the "D Dorian" mode uses all the same notes as C major (the white keys on a piano), but it begins with D. Compared with the Major (also known as "Ionian" mode), the Dorian sounds different, because relative to the root note D, it has a minor third and a minor seventh.
The best way to understand modes is to think of a toy piano where the black keys are just painted on - all you have are the white keys: C D E F G A B. Can you play a song that sounds like it's in a minor key? You can't play a song in C minor, because that would require three flats. So instead you play the song with A as the root (A B C D E F G). That scale is a mode of the major scale, called the Aeolian Mode.
When you play that minor scale, you're not playing "C minor", you're playing the relative minor of C, which is "A minor". Modes are relatives of each other if they have the same pattern of steps, starting on different steps.
To compute a mode of the current scale, we "rotate" all the notes down one semitone. Then if the rotated notes have an on bit in the root, then it is a mode of the original scale. It's as if you take the bracelet diagram that we've been using throughout this study, and twist it like a dial so that a different note is at the top, in the root position.
101010110101 = 2741 - major scale, "ionian" mode 110101011010 = 3418 - rotated down 1 semitone - not a scale 011010101101 = 1709 - rotated down 2 semitones - "dorian" 101101010110 = 2902 - rotated down 3 semitones - not a scale 010110101011 = 1451 - rotated down 4 semitones - "phrygian" 101011010101 = 2773 - rotated down 5 semitones - "lydian" 110101101010 = 3434 - rotated down 6 semitones - not a scale 011010110101 = 1717 - rotated down 7 semitones - "mixolydian" 101101011010 = 2906 - rotated down 8 semitones - not a scale 010110101101 = 1453 - rotated down 9 semitones - "aeolian" 101011010110 = 2774 - rotated down 10 semitones - not a scale 010101101011 = 1387 - rotated down 11 semitones - "locrian"
When we do this to every scale, we see modal relationships between scales, and we also discover symmetries when a scale is a mode of itself on another degree.
Prime Form
Often when discussing the properties of a scale, those properties (like interval distribution or evenness) are the same for all related scales, ie a scale, all its the modes, its inverse, and the modes of its inverse. In order to simplify things, it is useful to declare that one of those is the "prime form", so when doing analysis we discard all of them except one.
It's important to emphasize - because this point is sometimes missed - that the interval distribution in a scale is the same for all the scale's modes produced by rotation, but also for the scale's inverse produced by reflection. The prime form of a scale is chosen to represent the entire group of scales with equivalent interval patterns. In this study, prime scales are marked with a star .
In discussing Prime Form of a scale, we are undeniably treading into the topic of Pitch Class Sets, a more generalized study involving every possible combination of tones, regardless of the rules that make it a scale.
Forte vs Rahn
There are two dominant strategies for declaring the Prime Form of a set of tones; one was defined by Allen Forte2, and another similar one (with only subtle differences) described later by John Rahn3. While I have deep admiration for Forte's theoretical work, I prefer the Rahn prime formula, for the simple reason that the Rahn primes are the easier to calculate.
The calculation of the Prime Form according to Forte requires some inelegant cyclomatic complexity. Rahn's algorithm is slightly easier to do manually, and is simply the one with the lowest value when expressed in bits, as we have done in this study. This connection between Rahn's prime forms and the bit representation of a scale was proven in 2017 by brute force calculation of every possible scale and prime form according to all three algorithms.
In a necessarily succinct overview of this topic, I'll demonstrate the differences between Forte's algorithm and Rahn's. The prime form for pitch class sets is identical except for 6 sets. Both algorithms look at the distance between the first and last tones of the set, preferring the one with the smaller interval. In the case of a tie, this is where Forte and Rahn differ: Forte begins at the start of the set working toward the end, whereas Rahn starts at the end working toward the beginning.
Here are the six sets where Forte and Rahn disagree on which one is prime.
| Forte | Rahn |
|---|---|
{0,1,3,7,8} | {0,1,5,6,8} |
{0,1,3,5,8,9} | {0,1,4,5,7,9} |
{0,1,3,6,8,9} | {0,2,3,6,7,9} |
{0,1,2,4,7,8,9} | {0,1,2,5,6,7,9} |
{0,1,2,3,5,8,9} | {0,1,4,5,6,7,9} |
{0,1,2,4,5,7,9,10} | {0,1,3,4,5,7,8,10} |
A complete list of all modal families
Modal families with 3 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 3-12 | 273 Augmented Triad |
Modal families with 4 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 4-19 | 275 Dalic 305 Gonic 785 Aeoloric 2185 Dygic | 281 Lanic 401 Epogic 547 Pyrric 2321 Zyphic | |
| 4-20 | 291 Raga Lavangi 393 Lothic 561 Phratic 2193 Major Seventh | ||
| 4-24 | 277 Mixolyric 337 Kmhmu 4 Tone Type 2 1093 Lydic 1297 Aeolic | ||
| 4-27 | 293 Raga Haripriya 593 Saric 649 Byptic 1097 Aeraphic | 329 Lonic 553 Phradic 581 Bolic 1169 Raga Mahathi | |
| 4-26 | 297 Karen 4 Tone Type 3 549 Lahuzu 4 Tone Type 4 657 Lahuzu 4 Tone Type 3 1161 Bi Yu | ||
| 4-25 | 325 Messiaen Truncated Mode 6 1105 Messiaen Truncated Mode 6 Inverse | ||
| 4-28 | 585 Diminished Seventh |
Modal families with 5 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 5-13 | 279 Poditonic 369 Laditonic 1809 Ranitonic 2187 Ionothitonic 3141 Kanitonic | 285 Zaritonic 465 Zoditonic 1095 Phrythitonic 2595 Rolitonic 3345 Zylitonic | |
| 5-Z38 | 295 Gyritonic 625 Ionyptitonic 905 Bylitonic 2195 Zalitonic 3145 Stolitonic | 457 Staptitonic 569 Mothitonic 583 Aeritonic 2339 Raga Kshanika 3217 Molitonic | |
| 5-Z37 | 313 Goritonic 551 Aeoloditonic 913 Aeolyritonic 2323 Doptitonic 3209 Aeraphitonic | ||
| 5-15 | 327 Syptitonic 453 Raditonic 1137 Stonitonic 2211 Raga Gauri 3153 Zathitonic | ||
| 5-Z17 | 283 Aerylitonic 433 Raga Zilaf 1571 Lagitonic 2189 Zagitonic 2833 Dolitonic | ||
| 5-27 | 299 Raga Chitthakarshini 689 Raga Nagasvaravali 1417 Raga Shailaja 1573 Raga Guhamanohari 2197 Raga Hamsadhvani | 425 Raga Kokil Pancham 565 Aeolyphritonic 1165 Gycritonic 1315 Pyritonic 2705 Raga Mamata | |
| 5-26 | 309 Palitonic 849 Aerynitonic 1101 Stothitonic 1299 Aerophitonic 2697 Katagitonic | 345 Gylitonic 555 Aeolycritonic 1425 Ryphitonic 1605 Zanitonic 2325 Pynitonic | |
| 5-29 | 331 Raga Chhaya Todi 709 Raga Shri Kalyan 1201 Mixolydian Pentatonic 1577 Raga Chandrakauns 2213 Raga Desh | 421 Han-kumoi 653 Dorian Pentatonic 1129 Raga Jayakauns 1187 Kokin-joshi 2641 Raga Hindol | |
| 5-31 | 587 Pathitonic 601 Bycritonic 713 Thoptitonic 1609 Thyritonic 2341 Raga Priyadharshini | 589 Ionalitonic 617 Katycritonic 841 Phrothitonic 1171 Raga Manaranjani I 2633 Bartók Beta Chord | |
| 5-25 | 301 Raga Audav Tukhari 721 Raga Dhavalashri 1099 Dyritonic 1673 Thocritonic 2597 Raga Rasranjani | 361 Bocritonic 557 Raga Abhogi 1163 Raga Rukmangi 1681 Raga Valaji 2629 Raga Shubravarni | |
| 5-20 | 355 African Pentatonic 4 395 Phrygian Pentatonic 1585 Raga Khamaji Durga 2225 Ionian Pentatonic 2245 Raga Vaijayanti | 397 Aeolian Pentatonic 419 Hon-kumoi-joshi 1123 Iwato 2257 Lydian Pentatonic 2609 Raga Bhinna Shadja | |
| 5-28 | 333 Bogitonic 837 Epaditonic 1107 Mogitonic 1233 Ionoditonic 2601 Marga Hindolam | 357 Banitonic 651 Golitonic 1113 Locrian Pentatonic 2 1617 Phronitonic 2373 Dyptitonic | |
| 5-21 | 307 Raga Megharanjani 787 Aeolapritonic 817 Zothitonic 2201 Ionagitonic 2441 Kyritonic | 409 Laritonic 563 Thacritonic 803 Loritonic 2329 Styditonic 2449 Zacritonic | |
| 5-30 | 339 Zaptitonic 789 Zogitonic 1221 Epyritonic 1329 Epygitonic 2217 Kagitonic | 405 Raga Bhupeshwari 675 Altered Pentatonic 1125 Ionaritonic 1305 Dynitonic 2385 Karen 5tone Type 2 | |
| 5-32 | 595 Sogitonic 665 Raga Mohanangi 805 Rothitonic 1225 Raga Samudhra Priya 2345 Gothitonic | 613 Phralitonic 659 Raga Rasika Ranjani 809 Dogitonic 1177 Garitonic 2377 Bartók Gamma Chord | |
| 5-22 | 403 Raga Reva 611 Anchihoye 793 Mocritonic 2249 Raga Multani 2353 Raga Girija | ||
| 5-33 | 341 Bothitonic 1109 Kataditonic 1301 Koditonic 1349 Tholitonic 1361 Ngapauk auk Pyan | ||
| 5-34 | 597 Kung 681 Minor Added Sixth Pentatonic 1173 Dominant Pentatonic 1317 Chaio 1353 Raga Harikauns | ||
| 5-35 | 661 Major Pentatonic 677 Scottish Pentatonic 1189 Suspended Pentatonic 1193 Minor Pentatonic 1321 Blues Minor |
Modal families with 6 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 6-Z37 | 287 Gynimic 497 Kadimic 2191 Thydimic 3143 Polimic 3619 Thanimic 3857 Ponimic | ||
| 6-Z40 | 303 Golimic 753 Kytrimic 1929 Aeolycrimic 2199 Dyptimic 3147 Ryrimic 3621 Gylimic | 489 Phrathimic 573 Saptimic 1167 Aerodimic 2631 Macrimic 3363 Rogimic 3729 Starimic | |
| 6-Z39 | 317 Korimic 977 Kocrimic 1103 Lynimic 2599 Malimic 3347 Synimic 3721 Phragimic | 377 Kathimic 559 Lylimic 1937 Galimic 2327 Epalimic 3211 Epacrimic 3653 Sathimic | |
| 6-Z41 | 335 Zanimic 965 Ionothimic 1265 Pynimic 2215 Ranimic 3155 Ladimic 3625 Podimic | 485 Stoptimic 655 Kataptimic 1145 Zygimic 2375 Aeolaptimic 3235 Pothimic 3665 Stalimic | |
| 6-Z42 | 591 Gaptimic 633 Kydimic 969 Ionogimic 2343 Tharimic 3219 Ionaphimic 3657 Epynimic | ||
| 6-Z38 | 399 Zynimic 483 Kygimic 2247 Raga Vijayasri 2289 Mocrimic 3171 Zythimic 3633 Daptimic | ||
| 6-15 | 311 Stagimic 881 Aerothimic 1811 Kyptimic 2203 Dorimic 2953 Ionylimic 3149 Phrycrimic | 473 Aeralimic 571 Kynimic 1607 Epytimic 2333 Stynimic 2851 Katoptimic 3473 Lathimic | |
| 6-14 | 315 Stodimic 945 Raga Saravati 1575 Zycrimic 2205 Ionocrimic 2835 Ionygimic 3465 Katathimic | 441 Thycrimic 567 Aeoladimic 1827 Katygimic 2331 Dylimic 2961 Bygimic 3213 Eponimic | |
| 6-22 | 343 Ionorimic 1393 Mycrimic 1477 Raga Jaganmohanam 1813 Katothimic 2219 Phrydimic 3157 Zyptimic | 469 Katyrimic 1141 Rynimic 1309 Pogimic 1351 Aeraptimic 2723 Raga Jivantika 3409 Katanimic | |
| 6-Z46 | 599 Thyrimic 697 Lagimic 1481 Zagimic 1829 Pathimic 2347 Raga Viyogavarali 3221 Bycrimic | 629 Aeronimic 937 Stothimic 1181 Katagimic 1319 Phronimic 2707 Banimic 3401 Palimic | |
| 6-21 | 349 Borimic 1111 Sycrimic 1489 Raga Jyoti 1861 Phrygimic 2603 Gadimic 3349 Aeolocrimic | 373 Epagimic 1117 Raptimic 1303 Epolimic 1873 Dathimic 2699 Sythimic 3397 Sydimic | |
| 6-Z17 | 407 All-Trichord Hexachord 739 Rorimic 1817 Phrythimic 2251 Zodimic 2417 Kanimic 3173 Zarimic | 467 Raga Dhavalangam 797 Katocrimic 1223 Phryptimic 2281 Rathimic 2659 Katynimic 3377 Phralimic | |
| 6-Z47 | 663 Phrynimic 741 Gathimic 1209 Raga Bhanumanjari 1833 Ionacrimic 2379 Raga Gurjari Todi 3237 Raga Brindabani Sarang | 669 Gycrimic 933 Dadimic 1191 Pyrimic 1257 Blues Scale 2643 Raga Hamsanandi 3369 Mixolimic | |
| 6-Z45 | 605 Dycrimic 745 Kolimic 1175 Epycrimic 1865 Thagimic 2635 Gocrimic 3365 Katolimic | ||
| 6-16 | 371 Rythimic 791 Aeoloptimic 1841 Thogimic 2233 Donimic 2443 Panimic 3269 Raga Malarani | 413 Ganimic 931 Raga Kalakanthi 1127 Eparimic 2513 Aerycrimic 2611 Raga Vasanta 3353 Phraptimic | |
| 6-Z43 | 359 Bothimic 907 Tholimic 1649 Bolimic 2227 Raga Gaula 2501 Ralimic 3161 Kodimic | 461 Raga Syamalam 839 Ionathimic 1139 Aerygimic 2467 Raga Padi 2617 Pylimic 3281 Raga Vijayavasanta | |
| 6-Z44 | 615 Schoenberg Hexachord 825 Thyptimic 915 Raga Kalagada 2355 Raga Lalita 2505 Mydimic 3225 Ionalimic | 627 Mogimic 807 Raga Suddha Mukhari 921 Bogimic 2361 Docrimic 2451 Raga Bauli 3273 Raga Jivantini | |
| 6-18 | 423 Sogimic 909 Katarimic 1251 Sylimic 2259 Raga Mandari 2673 Mythimic 3177 Rothimic | 459 Zaptimic 711 Raga Chandrajyoti 1593 Zogimic 2277 Kagimic 2403 Lycrimic 3249 Raga Tilang | |
| 6-Z48 | 679 Lanimic 917 Dygimic 1253 Zolimic 1337 Epogimic 2387 Paptimic 3241 Dalimic | ||
| 6-7 | 455 Messiaen Mode 5 Rotation 2 2275 Messiaen Mode 5 3185 Messiaen Mode 5 Rotation 1 | ||
| 6-Z24 | 347 Barimic 1457 Raga Kamalamanohari 1579 Sagimic 1733 Raga Sarasvati 2221 Raga Sindhura Kafi 2837 Aelothimic | 437 Ronimic 1133 Stycrimic 1307 Katorimic 1699 Raga Rasavali 2701 Hawaiian 2897 Rycrimic | |
| 6-27 | 603 Aeolygimic 729 Stygimic 1611 Dacrimic 1737 Raga Madhukauns 2349 Raga Ghantana 2853 Baptimic | 621 Pyramid Hexatonic 873 Bagimic 1179 Sonimic 1683 Raga Malayamarutam 2637 Raga Ranjani 2889 Thoptimic | |
| 6-Z23 | 365 Marimic 1115 Superlocrian Hexamirror 1675 Raga Salagavarali 1745 Raga Vutari 2605 Rylimic 2885 Byrimic | ||
| 6-Z19 | 411 Lygimic 867 Phrocrimic 1587 Raga Rudra Pancama 2253 Raga Amarasenapriya 2481 Raga Paraju 2841 African Pentatonic 3 | 435 Raga Purna Pancama 795 Aeologimic 1635 Sygimic 2265 Raga Rasamanjari 2445 Zadimic 2865 Solimic | |
| 6-Z49 | 667 Rodimic 869 Kothimic 1241 Pygimic 1619 Prometheus Neapolitan 2381 Takemitsu Linea Mode 1 2857 Stythimic | ||
| 6-Z25 | 363 Soptimic 1419 Raga Kashyapi 1581 Raga Bagesri 1713 Raga Khamas 2229 Raga Nalinakanti 2757 Raga Nishadi | 429 Koptimic 1131 Honchoshi Plagal Form 1443 Raga Phenadyuti 1677 Raga Manavi 2613 Raga Hamsa Vinodini 2769 Dyrimic | |
| 6-Z28 | 619 Double-Phrygian Hexatonic 857 Aeolydimic 1427 Lolimic 1613 Thylimic 2357 Raga Sarasanana 2761 Dagimic | ||
| 6-Z26 | 427 Raga Suddha Simantini 1379 Kycrimic 1421 Raga Trimurti 1589 Raga Rageshri 2261 Raga Caturangini 2737 Raga Hari Nata | ||
| 6-34 | 683 Stogimic 1369 Boptimic 1381 Padimic 1429 Bythimic 1621 Scriabin's Prometheus 2389 Eskimo Hexatonic 2 | 853 Epothimic 1237 Salimic 1333 Lyptimic 1357 Takemitsu Linea Mode 2 1363 Gygimic 2729 Aeragimic | |
| 6-33 | 685 Raga Suddha Bangala 1195 Raga Gandharavam 1385 Phracrimic 1445 Raga Navamanohari 1685 Zeracrimic 2645 Raga Mruganandana | 725 Raga Yamuna Kalyani 1205 Raga Siva Kambhoji 1325 Phradimic 1355 Aeolorimic 1705 Raga Manohari 2725 Raga Nagagandhari | |
| 6-31 | 691 Raga Kalavati 811 Radimic 1433 Dynimic 1637 Syptimic 2393 Zathimic 2453 Raga Latika | 821 Aeranimic 851 Raga Hejjajji 1229 Raga Simharava 1331 Raga Vasantabhairavi 2473 Raga Takka 2713 Porimic | |
| 6-32 | 693 Arezzo Major Diatonic Hexachord 1197 Minor Hexatonic 1323 Ritsu 1449 Raga Gopikavasantam 1701 Mixolydian Hexatonic 2709 Raga Kumud | ||
| 6-30 | 715 T4 Prime Mode 1625 Hungarian Major No5 2405 T4 First Rotation | 845 Raga Neelangi 1235 Tritone Scale 2665 Messiaen Mode 2 Truncation 1 | |
| 6-Z50 | 723 Ionadimic 813 Larimic 1227 Thacrimic 1689 Lorimic 2409 Zacrimic 2661 Stydimic | ||
| 6-Z29 | 717 Raga Vijayanagari 843 Molimic 1203 Pagimic 1641 Bocrimic 2469 Raga Bhinna Pancama 2649 Aeolythimic | ||
| 6-20 | 819 Augmented Inverse 2457 Augmented | ||
| 6-35 | 1365 Whole Tone |
Modal families with 7 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 7-3 | 319 Epodian 1009 Katyptian 2207 Mygian 3151 Pacrian 3623 Aerocrian 3859 Aeolarian 3977 Kythian | 505 Sanian 575 Ionydian 2335 Epydian 3215 Katydian 3655 Mathian 3875 Aeryptian 3985 Thadian | |
| 7-9 | 351 Epanian 1521 Stanian 1989 Dydian 2223 Konian 3159 Stocrian 3627 Kalian 3861 Phroptian | 501 Katylian 1149 Bydian 1311 Bynian 2703 Galian 3399 Zonian 3747 Myrian 3921 Pythian | |
| 7-10 | 607 Kadian 761 Ponian 1993 Katoptian 2351 Gynian 3223 Thyphian 3659 Polian 3877 Thanian | 637 Debussy's Heptatonic 1001 Badian 1183 Sadian 2639 Dothian 3367 Moptian 3731 Aeryrian 3913 Bonian | |
| 7-8 | 381 Kogian 1119 Rarian 2001 Gydian 2607 Aerolian 3351 Crater Scale 3723 Myptian 3909 Rydian | ||
| 7-6 | 415 Aeoladian 995 Phrathian 2255 Dylian 2545 Thycrian 3175 Eponian 3635 Katygian 3865 Starian | 499 Ionaptian 799 Lolian 2297 Thylian 2447 Thagian 3271 Mela Raghupriya 3683 Dycrian 3889 Parian | |
| 7-Z12 | 671 Stycrian 997 Rycrian 1273 Heptatonic Blues 2383 Katorian 3239 Mela Tanarupi 3667 Kaptian 3881 Morian | ||
| 7-Z36 | 367 Aerodian 1777 Saptian 1931 Stogian 2231 Macrian 3013 Thynian 3163 Rogian 3629 Boptian | 493 Rygian 1147 Epynian 1679 Kydian 2621 Ionogian 2887 Gaptian 3491 Tharian 3793 Aeopian | |
| 7-16 | 623 Sycrian 889 Borian 1939 Dathian 2359 Gadian 3017 Gacrian 3227 Aeolocrian 3661 Mixodorian | 635 Epolian 985 Mela Sucaritra 1615 Sydian 2365 Sythian 2855 Epocrian 3475 Kylian 3785 Epagian | |
| 7-11 | 379 Aeragian 1583 Salian 1969 Zorian 2237 Epothian 2839 Lyptian 3467 Sudhvidhamagini 3781 Gyphian | 445 Gocrian 1135 Katolian 1955 Sonian 2615 Thoptian 3025 Epycrian 3355 Bagian 3725 Kyrian | |
| 7-14 | 431 Epyrian 1507 Zynian 1933 Mocrian 2263 Lycrian 2801 Zogian 3179 Daptian 3637 Raga Rageshri | 491 Aeolyrian 1423 Doptian 1597 Aeolodian 2293 Gorian 2759 Mela Pavani 3427 Zacrian 3761 Raga Madhuri | |
| 7-24 | 687 Aeolythian 1401 Pagian 1509 Ragian 1941 Aeranian 2391 Molian 3243 Mela Rupavati 3669 Mothian | 981 Mela Kantamani 1269 Katythian 1341 Madian 1359 Aerygian 2727 Mela Manavati 3411 Enigmatic 3753 Phraptian | |
| 7-23 | 701 Mixonyphian 1199 Magian 1513 Stathian 1957 Pyrian 2647 Dadian 3371 Aeolylian 3733 Gycrian | 757 Ionyptian 1213 Gyrian 1327 Zalian 1961 Soptian 2711 Stolian 3403 Bylian 3749 Raga Sorati | |
| 7-Z18 | 755 Phrythian 815 Bolian 1945 Zarian 2425 Rorian 2455 Bothian 3275 Mela Divyamani 3685 Kodian | 829 Lygian 979 Mela Dhavalambari 1231 Logian 2537 Laptian 2663 Lalian 3379 Verdi's Scala Enigmatica Descending 3737 Phrocrian | |
| 7-7 | 463 Zythian 967 Mela Salaga 2279 Dyrian 2531 Danian 3187 Koptian 3313 Aeolacrian 3641 Thocrian | 487 Dynian 911 Radian 2291 Zydian 2503 Mela Jhalavarali 3193 Zathian 3299 Syptian 3697 Ionarian | |
| 7-19 | 719 Kanian 971 Mela Gavambodhi 1657 Ionothian 2407 Zylian 2533 Podian 3251 Mela Hatakambari 3673 Ranian | 847 Ganian 973 Mela Syamalangi 1267 Katynian 2471 Mela Ganamurti 2681 Aerycrian 3283 Mela Visvambhari 3689 Katocrian | |
| 7-13 | 375 Sodian 1815 Godian 1905 Katacrian 2235 Bathian 2955 Thorian 3165 Mylian 3525 Zocrian | 477 Stacrian 1143 Styrian 1863 Pycrian 2619 Ionyrian 2979 Gyptian 3357 Phrodian 3537 Katogian | |
| 7-Z17 | 631 Zygian 953 Mela Yagapriya 1831 Pothian 2363 Kataptian 2963 Bygian 3229 Aeolaptian 3529 Stalian | ||
| 7-Z38 | 439 Bythian 1763 Katalian 1819 Pydian 2267 Padian 2929 Aeolathian 2957 Thygian 3181 Rolian | 475 Aeolygian 1595 Dacrian 1735 Mela Navanitam 2285 Aerogian 2845 Baptian 2915 Aeolydian 3505 Stygian | |
| 7-27 | 695 Sarian 1465 Mela Ragavardhani 1765 Lonian 1835 Byptian 2395 Zoptian 2965 Darian 3245 Mela Varunapriya | 949 Mela Mararanjani 1261 Modified Blues 1339 Kycrian 1703 Mela Vanaspati 2717 Epygian 2899 Kagian 3497 Phrolian | |
| 7-25 | 733 Donian 1207 Aeoloptian 1769 Blues Heptatonic II 1867 Solian 2651 Panian 2981 Ionolian 3373 Lodian | 749 Aeologian 1211 Ceiling Scale 1687 Phralian 1897 Ionopian 2653 Sygian 2891 Phrogian 3493 Rathian | |
| 7-21 | 823 Stodian 883 Ralian 1843 Ionygian 2459 Ionocrian 2489 Mela Gangeyabhusani 2969 Tholian 3277 Mela Nitimati | 827 Mixolocrian 947 Mela Gayakapriya 1639 Aeolothian 2461 Sagian 2521 Mela Dhatuvardhani 2867 Major Romani 3481 Katathian | |
| 7-26 | 699 Aerothian 1497 Mela Jyotisvarupini 1623 Lothian 1893 Ionylian 2397 Stagian 2859 Phrycrian 3477 Kyptian | 885 Sathian 1245 Lathian 1335 Elephant Scale 1875 Persichetti Scale 2715 Kynian 2985 Epacrian 3405 Stynian | |
| 7-Z37 | 443 Kothian 1591 Rodian 1891 Thalian 2269 Pygian 2843 Sorian 2993 Stythian 3469 Monian | ||
| 7-15 | 471 Dodian 1479 Mela Jalarnava 1821 Aeradian 2283 Aeolyptian 2787 Zyrian 3189 Aeolonian 3441 Thacrian | ||
| 7-29 | 727 Phradian 1483 Mela Bhavapriya 1721 Mela Vagadhisvari 1837 Dalian 2411 Aeolorian 2789 Zolian 3253 Mela Naganandini | 941 Mela Jhankaradhvani 1259 Stadian 1447 Mela Ratnangi 1693 Dogian 2677 Thodian 2771 Marva That 3433 Thonian | |
| 7-28 | 747 Lynian 1431 Phragian 1629 Synian 1881 Korian 2421 Malian 2763 Mela Suvarnangi 3429 Marian | 861 Rylian 1239 Epaptian 1491 Namanarayani 1869 Katyrian 2667 Byrian 2793 Eporian 3381 Katanian | |
| 7-30 | 855 Porian 1395 Locrian Dominant 1485 Minor Romani 1845 Mixolydian Augmented 2475 Neapolitan Minor 2745 Mela Sulini 3285 Lydian #6 | 939 Mela Senavati 1383 Pynian 1437 Sabach ascending 1653 Minor Romani Inverse 2517 Harmonic Lydian 2739 Mela Suryakanta 3417 Golian | |
| 7-33 | 1367 Leading Whole-Tone Inverse 1373 Storian 1397 Major Locrian 1493 Lydian Minor 1877 Aeroptian 2731 Neapolitan Major 3413 Leading Whole-tone | ||
| 7-20 | 743 Chromatic Hypophrygian Inverse 919 Chromatic Phrygian Inverse 1849 Chromatic Hypodorian Inverse 2419 Raga Lalita 2507 Todi That 3257 Mela Calanata 3301 Chromatic Mixolydian Inverse | 925 Chromatic Hypodorian 935 Chromatic Dorian 1255 Chromatic Mixolydian 2515 Chromatic Hypolydian 2675 Chromatic Lydian 3305 Chromatic Hypophrygian 3385 Chromatic Phrygian | |
| 7-22 | 871 Hungarian Romani Minor 4th Mode 923 Ultraphrygian 1651 Asian 2483 Double Harmonic 2509 Double Harmonic Minor 2873 Ionian Augmented Sharp 2 3289 Lydian Sharp 2 Sharp 6 | ||
| 7-31 | 731 Alternating Heptamode 1627 Hungarian Major 4th Mode 1739 Mela Sadvidhamargini 1753 Hungarian Major 2413 Harmonic Minor Flat 5 2861 Hungarian Major 5th Mode 2917 Nohkan Flute Scale | 877 Moravian Pistalkova 1243 Epylian 1691 Kathian 1747 Mela Ramapriya 2669 Jeths' Mode 2893 Lylian 2921 Pogian | |
| 7-32 | 859 Ultralocrian 1459 Phrygian Dominant 1643 Locrian Natural 6 1741 Lydian Diminished 2477 Harmonic Minor 2777 Aeolian Harmonic 2869 Major Augmented | 875 Locrian Double-flat 7 1435 Phrygian Flat 4 1645 Dorian Flat 5 1715 Harmonic Minor Inverse 2485 Harmonic Major 2765 Lydian Flat 3 2905 Lydian Augmented Sharp 2 | |
| 7-34 | 1371 Superlocrian 1389 Minor Locrian 1461 Major-Minor 1707 Dorian Flat 2 1749 Acoustic 2733 Melodic Minor Ascending 2901 Lydian Augmented | ||
| 7-35 | 1387 Locrian 1451 Phrygian 1453 Aeolian 1709 Dorian 1717 Mixolydian 2741 Major 2773 Lydian |
Modal families with 8 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 8-2 | 383 Logyllic 2033 Stolyllic 2239 Dacryllic 3167 Thynyllic 3631 Gydyllic 3863 Eparyllic 3979 Dynyllic 4037 Ionyllic | 509 Ionothyllic 1151 Mythyllic 2623 Aerylyllic 3359 Bonyllic 3727 Tholyllic 3911 Katyryllic 4003 Sadyllic 4049 Stycryllic | |
| 8-3 | 639 Ionaryllic 1017 Dythyllic 2367 Laryllic 3231 Kataptyllic 3663 Sonyllic 3879 Pathyllic 3987 Loryllic 4041 Zaryllic | ||
| 8-4 | 447 Thyphyllic 2019 Palyllic 2271 Poptyllic 3057 Phroryllic 3183 Mixonyllic 3639 Paptyllic 3867 Storyllic 3981 Phrycryllic | 507 Moryllic 1599 Pocryllic 2301 Bydyllic 2847 Phracryllic 3471 Gyryllic 3783 Phrygyllic 3939 Dogyllic 4017 Dolyllic | |
| 8-11 | 703 Aerocryllic 1529 Kataryllic 2021 Katycryllic 2399 Zanyllic 3247 Aeolonyllic 3671 Aeonyllic 3883 Kyryllic 3989 Sythyllic | 1013 Stydyllic 1277 Zadyllic 1343 Zalyllic 2719 Zocryllic 3407 Katocryllic 3751 Aerathyllic 3923 Stoptyllic 4009 Phranyllic | |
| 8-10 | 765 Mixonyphyllic 1215 Aeolanyllic 2025 Mixolydyllic 2655 Thocryllic 3375 Kygyllic 3735 Ionagyllic 3915 Gogyllic 4005 Phradyllic | ||
| 8-7 | 831 Rodyllic 1011 Kycryllic 2463 Ionathyllic 2553 Aeolaptyllic 3279 Pythyllic 3687 Zonyllic 3891 Ryryllic 3993 Ioniptyllic | ||
| 8-5 | 479 Kocryllic 1991 Phryptyllic 2287 Lodyllic 3043 Ionayllic 3191 Bynyllic 3569 Aeoladyllic 3643 Kydyllic 3869 Bygyllic | 503 Thoptyllic 1823 Phralyllic 2299 Phraptyllic 2959 Dygyllic 3197 Gylyllic 3527 Ronyllic 3811 Epogyllic 3953 Thagyllic | |
| 8-13 | 735 Sylyllic 1785 Tharyllic 1995 Sideways Scale 2415 Lothyllic 3045 Raptyllic 3255 Daryllic 3675 Monyllic 3885 Styryllic | 1005 Radyllic 1275 Stagyllic 1695 Phrodyllic 2685 Ionoryllic 2895 Aeragyllic 3495 Banyllic 3795 Epothyllic 3945 Lydyllic | |
| 8-12 | 763 Doryllic 1631 Rynyllic 2009 Stacryllic 2429 Kadyllic 2863 Aerogyllic 3479 Rothyllic 3787 Kagyllic 3941 Stathyllic | 893 Pycryllic 1247 Mygyllic 2003 Lolyllic 2671 Lylyllic 3049 Aeronyllic 3383 Daptyllic 3739 Ioninyllic 3917 Epaphyllic | |
| 8-Z15 | 863 Pyryllic 1523 Zothyllic 1997 Raga Cintamani 2479 Harmonic and Neapolitan Minor Mixed 2809 Gythyllic 3287 Phrathyllic 3691 Badyllic 3893 Phrocryllic | 1003 Ionyryllic 1439 Rolyllic 1661 Gonyllic 2549 Rydyllic 2767 Katydyllic 3431 Zyptyllic 3763 Modyllic 3929 Aeolothyllic | |
| 8-21 | 1375 Bothyllic 1405 Goryllic 1525 Sodyllic 2005 Gygyllic 2735 Gynyllic 3415 Ionaptyllic 3755 Phryryllic 3925 Thyryllic | ||
| 8-8 | 927 Koptyllic 999 Bylyllic 2511 Epyryllic 2547 Raga Ramkali 3303 Soptyllic 3321 Ionycryllic 3699 Aeolylyllic 3897 Locryllic | ||
| 8-6 | 495 Bocryllic 1935 Mycryllic 2295 Kogyllic 3015 Laptyllic 3195 Raryllic 3555 Pylyllic 3645 Zycryllic 3825 Pynyllic | ||
| 8-Z29 | 751 Epacryllic 1913 Zagyllic 1943 Malyllic 2423 Thorcryllic 3019 Mydyllic 3259 Loptyllic 3557 Thycryllic 3677 Katylyllic | 989 Phrolyllic 1271 Kolyllic 1871 Aeolyllic 2683 Thodyllic 2983 Zythyllic 3389 Socryllic 3539 Aeoryllic 3817 Zoryllic | |
| 8-14 | 759 Katalyllic 1839 Zogyllic 1977 Dagyllic 2427 Katoryllic 2967 Madyllic 3261 Dodyllic 3531 Neveseri 3813 Aeologyllic | 957 Phronyllic 1263 Stynyllic 1959 Katolyllic 2679 Rathyllic 3027 Rythyllic 3387 Aeryptyllic 3561 Pothyllic 3741 Zydyllic | |
| 8-18 | 879 Aeolocryllic 1779 Aerythyllic 1947 Ionoyllic 2487 Phroptyllic 2937 Aeolathyllic 3021 Gyptyllic 3291 Kodyllic 3693 Epaptyllic | 987 Aeraptyllic 1659 Magyllic 1743 Epigyllic 2541 Algerian 2877 Phrylyllic 2919 Molyllic 3507 Ponyllic 3801 Maptyllic | |
| 8-22 | 1391 Aeradyllic 1469 Epiryllic 1781 Lydian/Mixolydian Mixed 1963 Epocryllic 2743 Staptyllic 3029 Ionocryllic 3419 Magen Abot 1 3757 Raga Mian Ki Malhar | 1403 Espla's Scale 1517 Spanish Octamode 4th Rotation 1711 Adonai Malakh 1973 Spanish Octamode 6th Rotation 2749 Spanish Octamode 1st Rotation 2903 Spanish Octamode 10th Rotation 3499 Hamel 3797 Spanish Octamode 8th Rotation | |
| 8-17 | 891 Ionilyllic 1647 Polyllic 1971 Aerynyllic 2493 Manyllic 2871 Stanyllic 3033 Doptyllic 3483 Mugham Shüshtär 3789 Eporyllic | ||
| 8-16 | 943 Aerygyllic 1511 Styptyllic 1949 Mathyllic 2519 Dathyllic 2803 Raga Bhatiyar 3307 Boptyllic 3449 Bacryllic 3701 Bagyllic | 983 Epygyllic 1487 Lycryllic 1853 Phrynyllic 2539 Half-Diminished Bebop 2791 Ionyptyllic 3317 Lanyllic 3443 Verdi's Scala Enigmatica 3769 Aeracryllic | |
| 8-23 | 1455 Quartal Octamode 1515 Phrygian/Locrian Mixed 1725 Minor Bebop 1965 Raga Mukhari 2775 Quartal Octamode 10th Rotation 2805 Ichikotsuchô 3435 Prokofiev 3765 Dominant Bebop | ||
| 8-9 | 975 Messiaen Mode 4 Rotation 3 2535 Messiaen Mode 4 3315 Tcherepnin Octatonic Mode 1 3705 Messiaen Mode 4 Rotation 2 | ||
| 8-19 | 887 Sathyllic 1847 Thacryllic 1907 Lynyllic 2491 Layllic 2971 Aeolynyllic 3001 Lonyllic 3293 Saryllic 3533 Thadyllic | 955 Ionogyllic 1655 Katygyllic 1895 Salyllic 2525 Aeolaryllic 2875 Ganyllic 2995 Raga Saurashtra 3485 Sabach 3545 Thyptyllic | |
| 8-24 | 1399 Syryllic 1501 Stygyllic 1879 Mixoryllic 1909 Epicryllic 2747 Stythyllic 2987 Neapolitan Major and Minor Mixed 3421 Aerothyllic 3541 Racryllic | ||
| 8-20 | 951 Thogyllic 1767 Dyryllic 1851 Zacryllic 2523 Mirage Scale 2931 Zathyllic 2973 Panyllic 3309 Bycryllic 3513 Dydyllic | ||
| 8-27 | 1463 Zaptyllic 1757 Ionyphyllic 1771 Stylyllic 1883 Mixopyryllic 2779 Shostakovich 2933 Dalyllic 2989 Bebop Minor 3437 Gathyllic | 1499 Bebop Locrian 1723 JG Octatonic 1751 Aeolyryllic 1901 Ionidyllic 2797 Stalyllic 2909 Mocryllic 2923 Baryllic 3509 Stogyllic | |
| 8-26 | 1467 Spanish Phrygian 1719 Lyryllic 1773 Blues Scale II 1899 Moptyllic 2781 Gycryllic 2907 Magen Abot 2 2997 Major Bebop 3501 Gregorian Nr.4 | ||
| 8-25 | 1495 Messiaen Mode 6 Rotation 2 1885 Messiaen Mode 6 Rotation 1 2795 Van der Horst Octatonic 3445 Messiaen Mode 6 | ||
| 8-28 | 1755 Octatonic 2925 Diminished |
Modal families with 9 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 9-1 | 511 Chromatic Nonamode 2303 Nonatonic Chromatic 2 3199 Nonatonic Chromatic 3 3647 Nonatonic Chromatic 4 3871 Nonatonic Chromatic 5 3983 Nonatonic Chromatic 6 4039 Nonatonic Chromatic 7 4067 Nonatonic Chromatic 8 4081 Nonatonic Chromatic Descending | ||
| 9-2 | 767 Raptygic 2041 Aeolacrygic 2431 Gythygic 3263 Pyrygic 3679 Rycrygic 3887 Phrathygic 3991 Badygic 4043 Phrocrygic 4069 Starygic | 1021 Ladygic 1279 Sarygic 2687 Thacrygic 3391 Aeolynygic 3743 Thadygic 3919 Lynygic 4007 Doptygic 4051 Ionilygic 4073 Sathygic | |
| 9-3 | 895 Aeolathygic 2035 Aerythygic 2495 Aeolocrygic 3065 Zothygic 3295 Phroptygic 3695 Kodygic 3895 Eparygic 3995 Ionygic 4045 Gyptygic | 1019 Aeranygic 1663 Lydygic 2557 Dothygic 2879 Stadygic 3487 Byptygic 3791 Stodygic 3943 Zynygic 4019 Lonygic 4057 Phrygic | |
| 9-6 | 1407 Tharygic 1533 Katycrygic 2037 Sythygic 2751 Sylygic 3423 Lothygic 3759 Darygic 3927 Monygic 4011 Styrygic 4053 Kyrygic | ||
| 9-4 | 959 Katylygic 2023 Zodygic 2527 Phradygic 3059 Madygic 3311 Mixodygic 3577 Loptygic 3703 Katalygic 3899 Katorygic 3997 Dogygic | 1015 Ionodygic 1855 Marygic 2555 Bythygic 2975 Gaptygic 3325 Epygic 3535 Aeroptygic 3815 Mylygic 3955 Galygic 4025 Kalygic | |
| 9-7 | 1471 Radygic 1789 Blues Enneatonic II 2027 Boptygic 2783 Gothygic 3061 Apinygic 3439 Lythygic 3767 Chromatic Bebop 3931 Aerygic 4013 Raga Pilu | 1531 Styptygic 1727 Sydygic 2029 Kiourdi 2813 Zolygic 2911 Katygic 3503 Zyphygic 3799 Aeralygic 3947 Ryptygic 4021 Raga Pahadi | |
| 9-5 | 991 Aeolygic 1999 Zacrygic 2543 Dydygic 3047 Panygic 3319 Tholygic 3571 Dyrygic 3707 Rynygic 3833 Dycrygic 3901 Bycrygic | 1007 Ionycrygic 1951 Gonygic 2551 Zoptygic 3023 Aeracrygic 3323 Phrygygic 3559 Aerathygic 3709 Locrygic 3827 Dorygic 3961 Mixolydygic | |
| 9-8 | 1503 Padygic 1917 Sacrygic 2007 Stonygic 2799 Epilygic 3051 Stalygic 3447 Kynygic 3573 Kaptygic 3771 Stophygic 3933 Ionidygic | 1527 Aeolyrygic 1887 Aerocrygic 2013 Mocrygic 2811 Barygic 2991 Zanygic 3453 Katarygic 3543 Aeolonygic 3819 Aeolanygic 3957 Porygic | |
| 9-10 | 1759 Pylygic 1787 Mycrygic 2011 Raphygic 2927 Rodygic 2941 Laptygic 3053 Zycrygic 3511 Epolygic 3803 Epidygic 3949 Koptygic | ||
| 9-9 | 1519 Locrian/Aeolian Mixed 1967 Diatonic Dorian Mixed 1981 Houseini 2807 Zylygic 3031 Epithygic 3451 Garygic 3563 Ionoptygic 3773 Raga Malgunji 3829 Taishikicho | ||
| 9-11 | 1775 Lyrygic 1915 Thydygic 1975 Ionocrygic 2935 Modygic 3005 Gycrygic 3035 Gocrygic 3515 Moorish Phrygian 3565 Aeolorygic 3805 Moptygic | 1783 Youlan 1903 Diminishing Nonamode Basic 1979 Diminishing Nonamode 6th Rotation 2939 Diminishing Nonamode 2nd Rotation 2999 Diminishing Nonamode 3037 Nine Tone Scale 3517 Diminishing Nonamode 1st Rotation 3547 Diminishing Nonamode 9th Rotation 3821 Diminishing Nonamode 8th Rotation | |
| 9-12 | 1911 Messiaen Mode 3 Rotation 1 3003 Messiaen Mode 3 Rotation 2 3549 Messiaen Mode 3 |
Modal families with 10 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 10-1 | 1023 Chromatic Decamode 2559 Decatonic Chromatic 2 3327 Decatonic Chromatic 3 3711 Decatonic Chromatic 4 3903 Decatonic Chromatic 5 3999 Decatonic Chromatic 6 4047 Decatonic Chromatic 7 4071 Decatonic Chromatic 8 4083 Decatonic Chromatic 9 4089 Decatonic Chromatic Descending | ||
| 10-2 | 1535 Mixodyllian 2045 Katogyllian 2815 Aeradyllian 3455 Ryptyllian 3775 Loptyllian 3935 Kataphyllian 4015 Phradyllian 4055 Dagyllian 4075 Katyllian 4085 Sydyllian | ||
| 10-3 | 1791 Aerygyllian 2043 Lythyllian 2943 Dathyllian 3069 Bacryllian 3519 Raga Sindhi-Bhairavi 3807 Bagyllian 3951 Mathyllian 4023 Styptyllian 4059 Zolyllian 4077 Gothyllian | ||
| 10-4 | 1919 Rocryllian 2039 Danyllian 3007 Zyryllian 3067 Goptyllian 3551 Sagyllian 3581 Epocryllian 3823 Epinyllian 3959 Katagyllian 4027 Ragyllian 4061 Staptyllian | ||
| 10-5 | 1983 Soryllian 2031 Gadyllian 3039 Godyllian 3063 Solyllian 3567 Epityllian 3579 Zyphyllian 3831 Ionyllian 3837 Minor Pentatonic With Leading Tones 3963 Aeoryllian 4029 Major/Minor Mixed | ||
| 10-6 | 2015 Messiaen Mode 7 Rotation 4 3055 Messiaen Mode 7 3575 Messiaen Mode 7 Rotation 1 3835 Messiaen Mode 7 Rotation 2 3965 Messiaen Mode 7 Rotation 3 |
Modal families with 11 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 11-1 | 2047 Chromatic Undecamode 3071 Chromatic Undecamode 2 3583 Chromatic Undecamode 3 3839 Chromatic Undecamode 4 3967 Chromatic Undecamode 5 4031 Chromatic Undecamode 6 4063 Chromatic Undecamode 7 4079 Chromatic Undecamode 8 4087 Chromatic Undecamode 9 4091 Chromatic Undecamode 10 4093 Chromatic Undecamode 11 |
Modal families with 12 tones
| Forte Class Name | Prime and its rotations | Inverse and its rotations | |
|---|---|---|---|
| 12-1 | 4095 Chromatic |
Symmetry
There are two kinds of symmetry of interest to scale analysis. They are rotational symmetry and reflective symmetry.
Rotational Symmetry
Rotational symmetry is the symmetry that occurs by transposing a scale up or down by an interval, and observing whether the transposition and the original have an identical pattern of steps.
The set of 12 tones has 5 axes of symmetry. The twelve can be divided by 1, 2, 3, 4, and 6.
Any scale containing this kind of symmetry can reproduce its own tones by transposition, and is also called a "mode of limited transposition" (Messaien)
Below are all the scales that have rotational symmetry.
| axes of symmetry | interval of repetition | scales |
|---|---|---|
| 1,2,3,4,5,6,7,8,9,10,11 | semitone | |
| 2,4,6,8,10 | whole tone | |
| 3,6,9 | minor thirds | |
| 4,8 | major thirds | |
| 6 | tritones |
| number of notes in scale | Placement of rotational symmetries | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 1 | 0 | 0 | 3 | 0 | 0 | 1 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 0 | 1 | 0 | 3 | 0 | 10 | 0 | 3 | 0 | 1 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 2 | 0 | 0 | 10 | 0 | 0 | 2 | 0 | 0 | |
| 9 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 12 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
A curious numeric pattern
You'll notice that in the list of scales exhibiting rotational symmetry, many have a decimal representation that ends with the digit 5. A closer look shows that the pattern exists for all scales that have symmetry on axes of 6, 4, and 2 - where all the notes in the scale are in pairs a tritone apart. In the binary schema, each pair of notes that are a tritone apart add up to a multiple of 10, except for the root pair that adds up to 65. Therefore, all scales with rotational symmetry on the tritone will end with the digit 5.
1 + 64
= 65
2 + 128
= 130
4 + 256
= 260
8 + 512
= 520
16 + 1024
= 1040
32 + 2048
= 2080
Messiaen's Modes - and their truncations
The French composer Olivier Messiaen studied scales with rotational symmetry, because they are useful in creating sonorities with an ambiguous tonic. He famously named seven such modes, and asserted that they are the only ones that may exist; all other symmetrical scales are truncations of those. We can prove that Messiaen was correct, by putting every symmetrical scale into a chart of their truncation relationships.
In all of Messiaen's modes, the modes are regarded as identical, which makes sense because the whole point was to create ambiguous tonality. Therefore when we speak of one of the Messiaenic modes, we're talking about a whole modal family of scales, like this one which he labeled Mode 7:
Truncation is the process of removing notes from a scale, without affecting its symmetry. The concept is best explained by example. Let's take the mode which Messiaen called the Second Mode:
That scale is symmetrical along the axis of a 3-semitone interval, i.e. by transposing it up a minor third. When we remove tones to create a truncation, we must preserve that symmetry, by removing four notes from the scale, like this:
In addition to the 3-semitone symmetry, that scale is also symmetrical along the axis of a 6-semitone interval. We can create two different truncations of 1755 that preserve that symmetry:
Technically, all of Messiaen's modes are truncated forms of 4095 , the 12-tone scale, which is symmetrical at all intervals.
Hierarchy of truncations
This diagram illustrates that all symmetrical scales are truncations of the Messaienic modes (labeled "M" plus their number as assigned by Messaien). M1, M2, M3, and M7 are all truncations of the chromatic scale 4095; M2, M4, and M6 are truncations of M7; M1 and M5 are truncations of M6. M1 is also a truncation of M3, and M5 is also a truncation of M4. All the other rotationally symmetrical scales are labeled "T#" and are shown where they belong in the hierarchy of truncations.
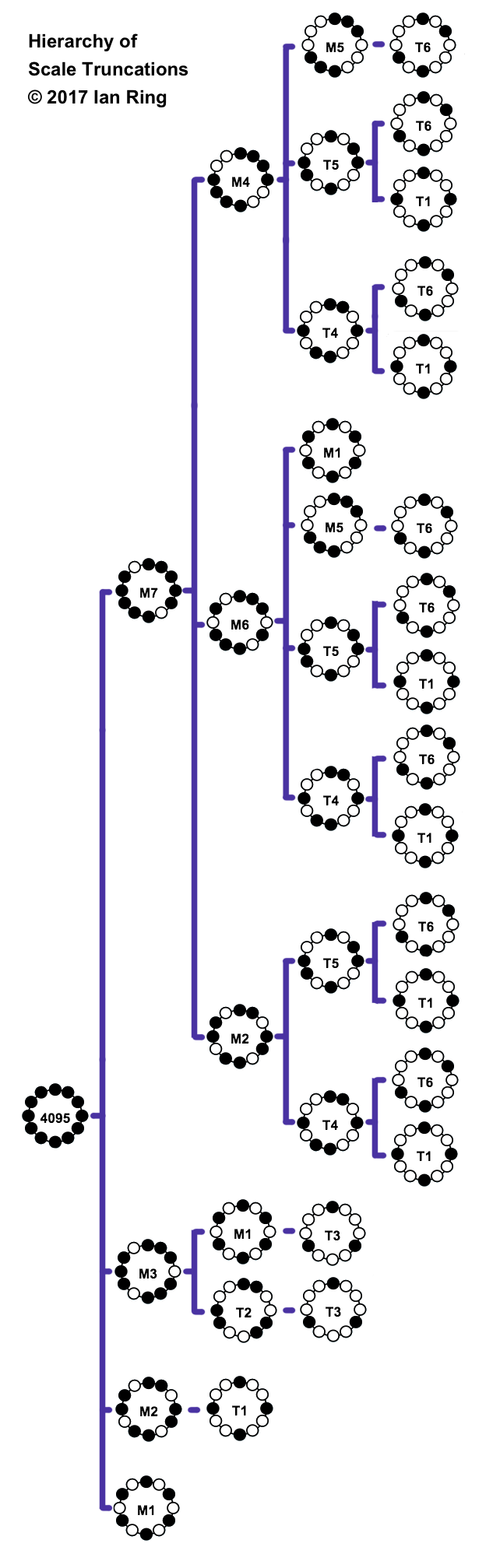
| Modal Family | Scales | is truncation of |
|---|---|---|
| * | ||
| Messiaen's Modes of Limited Transposition | ||
| M1 | *, M3, M6 | |
| M2 | *, M7 | |
| M3 | * | |
| M4 | M7 | |
| M5 | M6, M4 | |
| M6 | M7 | |
| M7 | * | |
| Truncations | ||
| T1 | M2, T5, T4 | |
| T2 | M3 | |
| T3 | M1, T2 | |
| T4 | M2, M6, M4 | |
| T5 | M2, M6, M4 | |
| T6 | T4, T5, M5, M1 | |
- In this study we are ignoring sonorities that aren't like a "scale" by disallowing large interval leaps (see the first section). If we ignore those rules, what other truncated sets exist? (spoiler hint: not very many!)
- Does the naming of certain scales by Messiaen seem haphazard? Why did he name M5, which is merely a truncation of both M6 and M4, which are in turn truncations of M7?
Reflective Symmetry
A scale can be said to have reflective symmetry if it has an axis of reflection. If that axis falls on the root, then the scale will have the same interval pattern ascending and descending. A reflectively symmetrical scale, symmetrical on the axis of the root tone, is called a palindromic scale.
Here are all the scales that are palindromic:
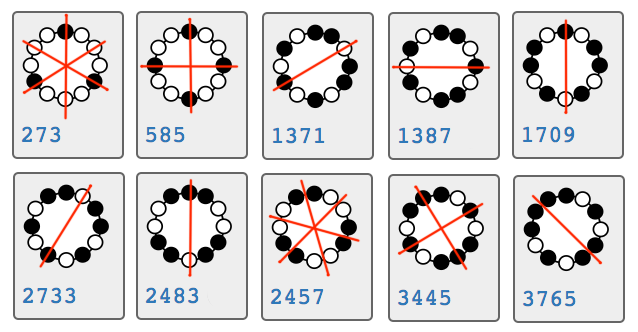
Chirality
An object is chiral if it is distinguishable from its mirror image, and can't be transformed into its mirror image by rotation. Chirality is an important concept in knot theory, and also has applications in molecular chemistry.
The concept of chirality is apparent when you consider "handedness" of a shape, such as a glove. A pair of gloves has a left hand and a right hand, and you can't transform a left glove into a right one by flipping it over or rotating it. The glove, therefore, is a chiral object. Conversely, a sock can be worn by the right or left foot; the mirror image of a sock would still be the same sock. Therefore a sock is not a chiral object.
Palindromic scales are achiral. But not all non-palindromic scales are chiral. For example, consider the scales 1105 and 325 (below). One is the mirror image (reflection) of the other. They are not palindromic scales. They are also achiral, because one can transform into the other by rotation.
The major scale is achiral. If you reflect the major scale, you get the phrygian scale; these two scales are modes (rotations) of each other. Therefore neither of them are chiral. Similarly, none of the other ecclesiastical major modes are chiral.
What makes chirality interesting? For one thing chirality indicates that a scale does not have any symmetry along any axis. If you examine all achiral scales, they will all have some axis of reflective symmetry - it's just not necessarily the root tone (which would make it palindromic).
A chiral object and its mirror image are called enantiomorphs. (source)
| Scale | Chirality / Enantiomorph |
|---|---|
| 273 Augmented Triad | achiral |
| 585 Diminished Seventh | achiral |
| 661 Major Pentatonic | achiral |
| 859 Ultralocrian | 2905 Lydian Augmented Sharp 2 |
| 1193 Minor Pentatonic | achiral |
| 1257 Blues Scale | 741 Gathimic |
| 1365 Whole Tone | achiral |
| 1371 Superlocrian | achiral |
| 1387 Locrian | achiral |
| 1389 Minor Locrian | achiral |
| 1397 Major Locrian | achiral |
| 1451 Phrygian | achiral |
| 1453 Aeolian | achiral |
| 1459 Phrygian Dominant | 2485 Harmonic Major |
| 1485 Minor Romani | 1653 Minor Romani Inverse |
| 1493 Lydian Minor | achiral |
| 1499 Bebop Locrian | 2933 Dalyllic |
| 1621 Scriabin's Prometheus | 1357 Takemitsu Linea Mode 2 |
| 1643 Locrian Natural 6 | 2765 Lydian Flat 3 |
| 1709 Dorian | achiral |
| 1717 Mixolydian | achiral |
| 1725 Minor Bebop | achiral |
| 1741 Lydian Diminished | 1645 Dorian Flat 5 |
| 1749 Acoustic | achiral |
| 1753 Hungarian Major | 877 Moravian Pistalkova |
| 1755 Octatonic | achiral |
| 2257 Lydian Pentatonic | 355 African Pentatonic 4 |
| 2275 Messiaen Mode 5 | achiral |
| 2457 Augmented | achiral |
| 2475 Neapolitan Minor | 2739 Mela Suryakanta |
| 2477 Harmonic Minor | 1715 Harmonic Minor Inverse |
| 2483 Double Harmonic | achiral |
| 2509 Double Harmonic Minor | achiral |
| 2535 Messiaen Mode 4 | achiral |
| 2731 Neapolitan Major | achiral |
| 2733 Melodic Minor Ascending | achiral |
| 2741 Major | achiral |
| 2773 Lydian | achiral |
| 2777 Aeolian Harmonic | 875 Locrian Double-flat 7 |
| 2869 Major Augmented | 1435 Phrygian Flat 4 |
| 2901 Lydian Augmented | achiral |
| 2925 Diminished | achiral |
| 2989 Bebop Minor | 1723 JG Octatonic |
| 2997 Major Bebop | achiral |
| 3055 Messiaen Mode 7 | achiral |
| 3411 Enigmatic | 2391 Molian |
| 3445 Messiaen Mode 6 | achiral |
| 3549 Messiaen Mode 3 | achiral |
| 3669 Mothian | 1359 Aerygian |
| 3765 Dominant Bebop | achiral |
| 4095 Chromatic | achiral |
- Reflective symmetry can occur with an axis on other notes of the scale. Are those interesting?
- The reflection axis can be on a tone, or between two tones. Is that interesting?
- Is there a more optimal or elegant way to find the reflective symmetry axes of a scale?
- Are there chiral enantiomorph pairs that are both named scales?
Combined Symmetry
Using similar methods to those above, we can identify all the scales that are both palindromic and have rotational symmetry. Here they are:
Balance
We assert a scale is "balanced", if the distribution of tones arranged around a 12-spoke wheel would balance on its centre. This is related to the well-known problem in mathematics known as the "balanced centrifuge problem".
There are 47 balanced scales. Here they are:
Interval Spectrum / Richness / Interval Vector
Howard Hanson, in the book "Harmonic Materials"4, posits that the character of a sonority is defined by the intervals that are within it. This definition is also called an "Interval Vector"5 or "Interval Class Vector" in Pitch Class Set theory. Furthermore, in his system an interval is equivalent to its inverse, i.e. the sonority of a perfect 5th is the same as the perfect 4th. Hanson categorizes all intervals as being one of six classes, and gives each a letter: p m n s d t, ordered from most consonant (p) to most dissonant (t). When an interval appears more than once in a sonority, it is superscripted with a number, like p2.
P - the Perfects (5 or 7)
This is the interval of a perfect 5th, or perfect 4th.
M - The Major Third (4 or 8)
This is the interval of a major 3rd, or minor 6th
N - The Minor Third (3 or 9)
This is the interval of a minor 3rd, or a major 6th
S - the second (2 or 10)
This is the interval of a major 2nd, or minor 7th
D - the Diminished (1 or 11)
Intervals of a minor 2nd, or a major 7th
T - the Tritone (6 semitones)
For example, in Hanson's analysis, a C major triad has the sonority pmn, because it contains one perfect 5th between the C and G (p), a major third between C and E (m), and a minor third between the E and G (n). Interesting to note that a minor triad of A-C-E is also a pmn sonority, just with the arrangement of the minor and major intervals swapped. The diminished seventh chord 585 has the sonority n4t2 because it contains four different minor thirds, and two tritones.
We can count the appearances of an interval using a method called "cyclic autocorrelation6". To find out how many of interval X appear in a scale, we rotate a copy of the scale by X degrees, and then count the number of positions where an "on" bit appears in both the original and copy.
All members of the same modal family will have the same interval spectrum, because the spectrum doesn't care about rotation, and modes are merely rotations of each other. And there will be many examples of different families that have the same interval spectrum - for example, 281 and 275 both have the spectrum "pm3nd", but they are not modes of each other.
Below is a table of some of the named scales, and their interval spectrum. You'll notice that modal families will all have the same spectrum; hence every named mode of the diatonic scale (lydian, dorian, phrygian etc.) has the same spectrum of p6m3n4s5d2t
| Scale | Spectrum (Hanson) | Vector (modern) |
|---|---|---|
| 273 Augmented Triad | m3 | 000300 |
| 585 Diminished Seventh | n4t2 | 004002 |
| 661 Major Pentatonic | p4mn2s3 | 032140 |
| 859 Ultralocrian | p4m4n5s3d3t2 | 335442 |
| 1193 Minor Pentatonic | p4mn2s3 | 032140 |
| 1257 Blues Scale | p4m2n3s3d2t | 233241 |
| 1365 Whole Tone | m6s6t3 | 060603 |
| 1371 Superlocrian | p4m4n4s5d2t2 | 254442 |
| 1387 Locrian | p6m3n4s5d2t | 254361 |
| 1389 Minor Locrian | p4m4n4s5d2t2 | 254442 |
| 1397 Major Locrian | p2m6n2s6d2t3 | 262623 |
| 1451 Phrygian | p6m3n4s5d2t | 254361 |
| 1453 Aeolian | p6m3n4s5d2t | 254361 |
| 1459 Phrygian Dominant | p4m4n5s3d3t2 | 335442 |
| 1485 Minor Romani | p4m5n3s4d3t2 | 343542 |
| 1493 Lydian Minor | p2m6n2s6d2t3 | 262623 |
| 1499 Bebop Locrian | p5m5n6s5d4t3 | 456553 |
| 1621 Scriabin's Prometheus | p2m4n2s4dt2 | 142422 |
| 1643 Locrian Natural 6 | p4m4n5s3d3t2 | 335442 |
| 1709 Dorian | p6m3n4s5d2t | 254361 |
| 1717 Mixolydian | p6m3n4s5d2t | 254361 |
| 1725 Minor Bebop | p7m4n5s6d4t2 | 465472 |
| 1741 Lydian Diminished | p4m4n5s3d3t2 | 335442 |
| 1749 Acoustic | p4m4n4s5d2t2 | 254442 |
| 1753 Hungarian Major | p3m3n6s3d3t3 | 336333 |
| 1755 Octatonic | p4m4n8s4d4t4 | 448444 |
| 2257 Lydian Pentatonic | p3m2nsd2t | 211231 |
| 2275 Messiaen Mode 5 | p4m2s2d4t3 | 420243 |
| 2457 Augmented | p3m6n3d3 | 303630 |
| 2475 Neapolitan Minor | p4m5n3s4d3t2 | 343542 |
| 2477 Harmonic Minor | p4m4n5s3d3t2 | 335442 |
| 2483 Double Harmonic | p4m5n4s2d4t2 | 424542 |
| 2509 Double Harmonic Minor | p4m5n4s2d4t2 | 424542 |
| 2535 Messiaen Mode 4 | p6m4n4s4d6t4 | 644464 |
| 2731 Neapolitan Major | p2m6n2s6d2t3 | 262623 |
| 2733 Melodic Minor Ascending | p4m4n4s5d2t2 | 254442 |
| 2741 Major | p6m3n4s5d2t | 254361 |
| 2773 Lydian | p6m3n4s5d2t | 254361 |
| 2777 Aeolian Harmonic | p4m4n5s3d3t2 | 335442 |
| 2869 Major Augmented | p4m4n5s3d3t2 | 335442 |
| 2901 Lydian Augmented | p4m4n4s5d2t2 | 254442 |
| 2925 Diminished | p4m4n8s4d4t4 | 448444 |
| 2989 Bebop Minor | p5m5n6s5d4t3 | 456553 |
| 2997 Major Bebop | p6m5n6s5d4t2 | 456562 |
| 3055 Messiaen Mode 7 | p8m8n8s8d8t5 | 888885 |
| 3411 Enigmatic | p4m4n3s5d3t2 | 353442 |
| 3445 Messiaen Mode 6 | p4m6n4s6d4t4 | 464644 |
| 3549 Messiaen Mode 3 | p6m9n6s6d6t3 | 666963 |
| 3669 Mothian | p4m4n3s5d3t2 | 353442 |
| 3765 Dominant Bebop | p7m4n5s6d4t2 | 465472 |
| 4095 Chromatic | p12m12n12s12d12t6 | 12121212126 |
- Is there an optimal or elegant way to find all scales with a given spectrum?
- What patterns appear in interval distribution?
- Which are the most common, and least common spectra?
Deep Scales
A "deep" scale is one for which the interval vector consists of unique values. There are only two Prime Deep Scales, and all their rotations and reflections will also be Deep. One of them is the major diatonic collection, and the other is the major scale with the leading tone omitted. Here they are:
Evenness
Another interesting property of a scale is whether the notes are evenly spaced, or clumped together. The theory of musical scale evenness owes to "Diatonic Set Theory", the work of Richard Krantz and Jack Douhett7. In their paper, they explain how you can determine the "evenness" of a scale, first by establishing the intervals between each note and every other.
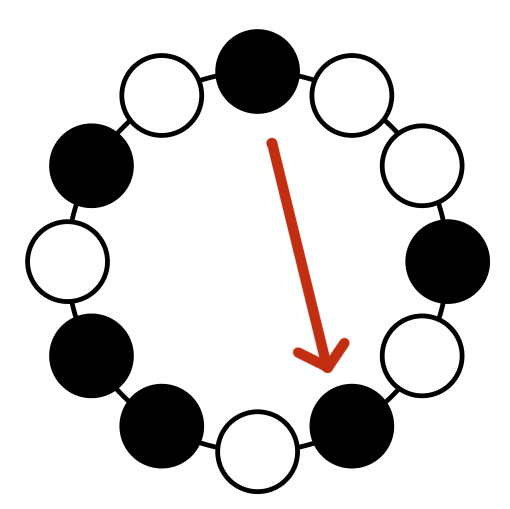
To measure the evenness of the scale, the first step is to build the distribution spectra. The spectra shows the distinct specific intervals between notes, for each generic interval of the scale. Each spectrum is notated like this:
<generic interval> = { specific interval, specific interval, ...}
The number in angle brackets is the generic interval, ie we are asking "for notes that are this many steps away in the scale". The numbers in curly brackets are the specific intervals we find present for those steps, ie "between those steps we find notes that are this many semitones apart".
It's best explained with an example. Below is the scale bracelet diagram and distribution spectra for Scale 1449:
| Scale | Notes | Distribution Spectra |
|---|---|---|
| <1> = {1,2,3} <2> = {3,4,5} <3> = {5,7} <4> = {7,8,9} <5> = {9,10,11} |
In line 1, the first spectrum, <1> indicates that we are looking at notes that are one scale step away from each other. We have notes that are one semitone apart (eg G and G#), two semitones (D# and F), and three semitones (C and D#). Duplicates of these are ignored; we merely want to know what intervals are present, not how many of them exist.
In line 2, the second spectrum, <2> indicates that we are looking at notes that are two scale steps away from each other. We see pairs that are three semitones apart (eg F and G#), four semitones (D# and G), and five semitones (C and F).
When there is more than one specific interval, the spectrum width is the difference between the largest and smallest value. For example for the <3> spectrum above, the specific intervals are {5,7} and so its width is 2, which is 7 minus 5.
The spectrum variation is the sum of all those widths, divided by the number of tones.
Once the distribution specta are built, we analyze them to discover interesting properties of the scale. For instance,
- If all the spectra have just one specific interval, then the scale has exactly equal distribution
- If the spectra have two intervals with a difference no greater than one, then the scale is maximally even - it's distributed as evenly as it can be with no room for improvement.
- If the spectra has any widths greater than 1, then it's not maximally even.
- If there are exactly two specific intervals in all the spectra, then the scale is said to have Myhill's property.
Ultimately, the measure of a scale's evenness is its Spectra Variation. We add up all the spectrum widths, and divide by the number of tones in the scale, to achieve an average width with respect to the scale size. If a scale has perfectly spaced notes with completely uniform evenness, then it has a spectra variation of zero. A higher variation means the scale distribution is less even.
The following four scales have a perfect score - a spectra variation of zero:
Obviously, it is possible to evenly distribute 6 tones around a 12-tone scale. But it is impossible to do that with a 5 tone (pentatonic) or 7 tone (heptatonic) scale. For such tone counts all we can hope to achieve is an optimally even distribution.
Below are all the prime scales (ie with rotations and reflections omitted), sorted from most even to least even. If you click to each scale detail page, you can read its spectra variation there.
3 tones
4 tones
5 tones
6 tones
7 tones
8 tones
9 tones
10 tones
11 tones
12 tones
Myhill's Property
Myhill's Property is the quality of a pitch class set where the spectrum has exactly two specific intervals for every generic interval. There are 6 prime scales with Myhill's property.
There is a chapter all about the Myhill Property - and why it mattters - in the book.
Propriety
In the section about evenness, we discussed the concepts of Generic Intervals and Specific Intervals. There is a property of a scale named "Propriety", which indicates whether the relation between generic and specific intervals is ambiguous or not. This property was discovered by David Rothenberg in 1978, so it is sometimes called "Rothenberg Propriety".
Rothenberg stated that there are three levels of propriety. At the most exclusive level, there are those whose specific intervals have an unambiguous relationship to the generic scale steps; these are called Strictly Proper. An easy example of a strictly proper scale is the 12-tone chromatic scale. If you hear an interval of 3 semitones, you know without any doubt that it is the generic distance of 3 scale steps. Any specific interval of 7 semitones is without any ambiguity going to be a generic interval of 7 scale steps. And so on.
Strictly proper scales are not common. Since all transformations of a scale have the same propriety, here we will only look at prime scales. Here are all the strictly proper ones:
Rothenberg defined that below these strictly proper scales, there is a strata of scales that are merely proper, bur not strictly so. To be proper, a specific interval can describe two different generic intervals, but there mustn't be any overlap. Stated another way, in a proper scale, there should never be a generic 4th that is smaller than a generic 3rd; but they might be the same size. The collection of proper scales is larger than the strict collection, but it's still an exclusive club. Here are all the prime scales that are proper but not strictly so:
Lastly, there are all the other scales that aren't proper at all; these are Improper Scales. Those scales will all have interval overlapping, where there the size of a generic interval does not assure that it is specifically larger or smaller than another generic interval.
You can judge the propriety of a scale by inspecting its distribution spectra. Look at this scale:
| Scale | Notes | Distribution Spectra |
|---|---|---|
| <1> = {1,2,3} <2> = {3,4,5} <3> = {5,7} <4> = {7,8,9} <5> = {9,10,11} |
Observe the spectrum of each generic interval, and how the specific intervals fit into niches. The specific interval of 3 semitones could be <1> or <2>. The specific interval of 5 semitones could be <2> or <3>, and so on. The generic ranges meet and share common edges, but they do not overlap. That means this scale is proper, but it is not strictly proper.
Next, we'll look at an example of an improper scale, the Neapolitan Minor.
| Scale | Notes | Distribution Spectra |
|---|---|---|
| <1> = {1,2,3} <2> = {2,3,4} <3> = {4,5,6} <4> = {6,7,8} <5> = {8,9,10} <6> = {9,10,11} |
The impropriety of this scale is evident in two of its specific intervals. In Neapolitan Minor, it is possible to have a generic interval of two scale steps with a specific interval of 2 (between B and D flat), which is smaller than a generic interval of one step with a specific interval of 3 (between A flat and B). The fact that a 2nd can be larger than a 3rd means this scale is not proper. The same situation exists where a generic interval of 5 scale steps can have a specific interval of 10, while a generic interval of 6 can have an interval of 9. This "overlap" of specific intervals in the distribution spectra indicates that this scale is improper.
You might think, what's the big deal here? The deal is that when we list the strictly proper and proper scales, they include all the diatonic modes, common scales like whole tone and the more typical pentatonics, consonant scales that are typically used in music. The Propriety of a scale is a good indicator of "sounds good", and yet it's a measurement that has no basis in the harmonic series, which most other theories rely on for the notion of consonance. Propriety also has no reliance on the tuning system being comprised of 12 equal semitones. Because of this interesting observation of interval distribution patterns, propriety can be applied to tuning systems of more than (or less than) 12 tones, to pick out scales that are likely to have meaningful potential for music-making.
Maximal Area
Maximal Area is a property invented by David Rappaport8. He observed that along with the maximally even sets, there are popular scales that share a similar composition of intervals, but not in their most evenly spaced configuration. Rappaport observed that when tones of a scale are arranged around a circle, the interior area of a polygon with vertices at each tone describes a "score" that favours popular scales. Every scale with maximal evenness will also have maximal area, but not all scales with maximal area are maximally even.
Note that the interior area for a scale is identical for all transpositions and inversions of a scale, so it suffices to measure the area for prime scales only. While for each cardinality there will be only one prime set that has maximal evenness, there may be multiple prime sets that share the same maximal area. Here they are.
| Cardinality | Interior Area | Sets |
|---|---|---|
| 3 tones | 1.299 | 273 Augmented Triad |
| 4 tones | 2 | 585 Diminished Seventh |
| 5 tones | 2.299 | 597 Kung 661 Major Pentatonic |
| 6 tones | 2.598 | 1365 Whole Tone |
| 7 tones | 2.665 | 1367 Leading Whole-Tone Inverse 1371 Superlocrian 1387 Locrian |
| 8 tones | 2.732 | 1375 Bothyllic 1391 Aeradyllic 1399 Syryllic 1455 Quartal Octamode 1463 Zaptyllic 1467 Spanish Phrygian 1495 Messiaen Mode 6 Rotation 2 1755 Octatonic |
| 9 tones | 2.799 | 1407 Tharygic 1471 Radygic 1503 Padygic 1519 Locrian/Aeolian Mixed 1759 Pylygic 1775 Lyrygic 1911 Messiaen Mode 3 Rotation 1 |
| 10 tones | 2.866 | 1535 Mixodyllian 1791 Aerygyllian 1919 Rocryllian 1983 Soryllian 2015 Messiaen Mode 7 Rotation 4 |
| 11 tones | 2.933 | 2047 Chromatic Undecamode |
| 12 tones | 3 | 4095 Chromatic |
Hemitonia and Tritonia
One interesting approach to understanding scales is to look at the distribution of consonant and dissonant intervals in the scale. We did this already in the "spectrum analysis" above, but two intervals in particular are commonly regarded in more depth: tritones and semitones - which are deemed the most dissonant of intervals, and those that give a scale its spice and flavour.
A scale that contains semitones is called "hemitonic", and we will also refer to a hemitonic as the scale member that has the upper semitone neighbour (for example, mi-fa and ti-do in a major scale, the hemitones are mi and fa).
A scale that contains tritones is called "tritonic", and we will also refer to a tritonic as the scale member that has a tritone above it. This concept seems very close to the notion of "imperfection" (explained below)
Since hemitonia and tritonia are based on the interval spectrum, all the modes of a scale will have the same hemitonia. For example, the major scale is dihemitonic and ancohemitonic; thus so are dorian, phrygian, lydian, etc.
| Number of tones | # of Hemitonic Scales | # of Tritonic Scales |
|---|---|---|
| 3 | 0 | 0 |
| 4 | 12 | 24 |
| 5 | 140 | 150 |
| 6 | 335 | 335 |
| 7 | 413 | 413 |
| 8 | 322 | 322 |
| 9 | 165 | 165 |
| 10 | 55 | 55 |
| 11 | 11 | 11 |
| 12 | 1 | 1 |
It's well to know that so many scales are hemitonic and tritonic (having more than zero semitones or tritones), but obviously some scales are more hemitonic than others. A scale could have no hemitonics ("ahemitonic"), one ("unihemitonic"), two ("dihemitonic"), three ("trihemitonic") and so on. Let's look at the count of hemitones in our scales.
Number of hemitones tones in scale
0 1 2 3 4 5 6 7 8 9 10 11 12 3 1 0 0 0 0 0 0 0 0 0 0 0 0 4 19 12 0 0 0 0 0 0 0 0 0 0 0 5 15 80 60 0 0 0 0 0 0 0 0 0 0 6 1 30 150 140 15 0 0 0 0 0 0 0 0 7 0 0 21 140 210 42 0 0 0 0 0 0 0 8 0 0 0 0 70 168 84 0 0 0 0 0 0 9 0 0 0 0 0 0 84 72 9 0 0 0 0 10 0 0 0 0 0 0 0 0 45 10 0 0 0 11 0 0 0 0 0 0 0 0 0 0 11 0 0 12 0 0 0 0 0 0 0 0 0 0 0 0 1
Fun fact: there are no scales with 11 hemitones. Do you understand why?
| Number of tritones | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tones in scale | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 7 | 16 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 5 | 40 | 75 | 30 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 1 | 12 | 102 | 146 | 69 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 14 | 112 | 196 | 84 | 7 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 62 | 168 | 84 | 8 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 84 | 72 | 9 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 45 | 10 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Cohemitonia
Cohemitonia is the presense of two semitones consecutively in scale order. For instance, if a scale has three cromatically consecutive notes, then it is cohemitonic. We will also refer to the cehemitonic as the tone that has two semitone neighbours above it.
Proximity
We would consider two scales to be "near" each other, if they bear many similarities; sharing many of the same notes, such that it would take few mutations to turn one into the other.
This distance measured by mutation is almost the same thing as a "Levenshtein Distance". The normal definition of a Levenshtein Distance on a string of characters allows three kinds of mutation: insertion, deletion, and substitution. Our scale mutations are different from a string mutation, in that scales can't do substitution, instead we move tones up or down with rules for handling collision. This difference means we can't employ all the elegant formulas bequeathed to us by Vladimir Levenshtein.
We can mutate a scale in three ways:
- Move a tone up or down by a semitone
- Remove a tone
- Add a tone
It is simple to generate all the scales at a distance of 1, just by performing all possible mutations to every interval above the root.
Example
Here are all the scales that are a distance of 1 from the major scale, aka 2741 , shown here as a simple C major scale:
| add a tone at C# |  | 2743 Staptyllic |
| lower the D to D♭ | 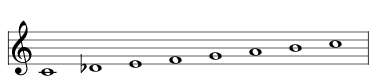 | 2739 Mela Suryakanta |
| raise the D to D# | 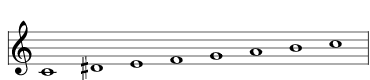 | 2745 Mela Sulini |
| delete the D | 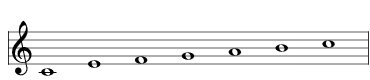 | 2737 Raga Hari Nata |
| add a tone at D# |  | 2749 Spanish Octamode 1st Rotation |
| lower the E to E♭ | 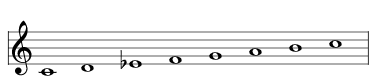 | 2733 Melodic Minor Ascending |
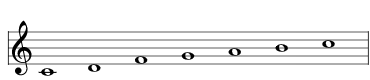 | same as deleting E | |
| delete the E |  | 2725 Raga Nagagandhari |
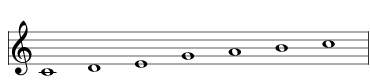 | same as deleting F | |
| raise the F to F# |  | 2773 Lydian |
| delete the F |  | 2709 Raga Kumud |
| add a tone at F# |  | 2805 Ichikotsuchô |
| lower the G to G♭ | 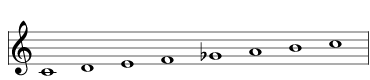 | 2677 Thodian |
| raise the G to G# | 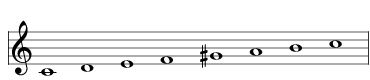 | 2869 Major Augmented |
| delete the G | 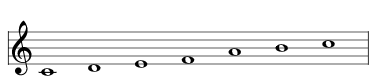 | 2613 Raga Hamsa Vinodini |
| add a tone at G# | 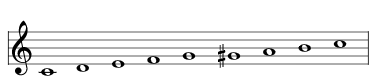 | 2997 Major Bebop |
| lower the A to A♭ | 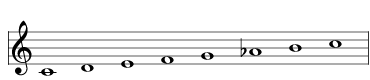 | 2485 Harmonic Major |
| raise the A to A# | 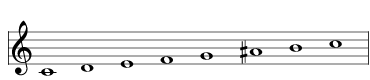 | 3253 Mela Naganandini |
| delete the A | 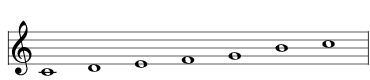 | 2229 Raga Nalinakanti |
| add a tone at A# | 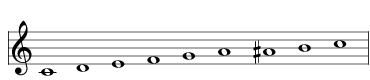 | 3765 Dominant Bebop |
| lower the B to B♭ | 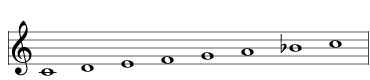 | 1717 Mixolydian |
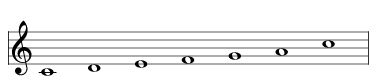 | same as deleting B | |
| delete the B |  | 693 Arezzo Major Diatonic Hexachord |
Evidently since every scale will have a collection of neighbours similar to this one, a complete graph of scale proximity is large, but not unfathomably so.
We can also easily calculate the Levenshtein distance between two scales. Apply an XOR operation to expose changed bits between two scales. Adjacent on bits in the XOR where the bits were different in the original scale identify a "move" operation. Any bits remaining are either an addition or deletion.
Imperfection
Imperfection is a concept invented (so far as I can tell) by William Zeitler, to describe the presence or absense of perfect fifths in the scale tones. Any tone in the scale that does not have the perfect fifth above it represented in the scale is an "imperfect" tone. The number of imperfections is a metric that plausibly correlates with the perception of dissonance in a sonority.
The only scale that has no imperfections is the 12-tone chromatic scale.
This table differs from Zeitler's9, because this script does not de-duplicate modes. If an imperfection exists in a scale, it will also exist in all the sibling modes of that scale. Hence the single imperfect tone in the 11-tone scale is found 11 times (in 11 scales that are all modally related), whereas Zeitler only counts it as one.
| number of notes in scale | # of Imperfections | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||||
| 4 | 0 | 0 | 8 | 16 | 7 | 0 | 0 | ||||
| 5 | 0 | 5 | 30 | 75 | 40 | 5 | 0 | ||||
| 6 | 0 | 6 | 69 | 146 | 102 | 12 | 1 | ||||
| 7 | 0 | 7 | 84 | 196 | 112 | 14 | 0 | ||||
| 8 | 0 | 8 | 84 | 168 | 62 | 0 | 0 | ||||
| 9 | 0 | 9 | 72 | 84 | 0 | 0 | 0 | ||||
| 10 | 0 | 10 | 45 | 0 | 0 | 0 | 0 | ||||
| 11 | 0 | 11 | 0 | 0 | 0 | 0 | 0 | ||||
| 12 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
Going Further
- Looking at the table, there are 5 scales of 5 tones with one imperfection. There are 6 scales of 6 tones with only one imperfection. The same patten continues right up to 11 tones. What causes this pattern?
- The only 7-note scale with only one imperfection is the major diatonic scale (plus all its modes). Is it a coincidence that we find this scale sonically pleasing?
Negative
One peculiar way we can manipulate a scale is to "flip its bits" -- so that every bit that is on becomes off, and all that were of are turned on. If you flip a scale with a root tone, you will get a non-scale without a root tone; so it's not so useful to speak of negating a scale, instead we negate an entire modal family to find the modal family that is its negative.
For example, one that's easy to conceptualize is the major scale, which (in C) occupies all the white keys on a piano. The negative of the major scale is all the notes that aren't in the major scale - just the black keys, which interestingly have the pattern of a major pentatonic (with F# as the root). In pitch class set theory, the negative of a set is called its "complement", and Dr Forte named complementary pairs with matching numbers.
Glossary
- TET
- Twelve-tone Equal Temperament. The system in which our octave is split into twelve equal intervals.
- achiral
- Not having chirality, i.e. the mirror image can be achieved by rotation.
- ancohemitonic
- A scale that is not cohemitonic. This either means it contain no semitones (and thus is anhemitonic), or contain semitones (being hemitonic) where none of the semitones appear consecutively in scale order.
- anhemitonic
- A scale that does not include any semitones
- atritonic
- Containing no tritones
- balance
- Having tones distributed such that if they were equal weights distributed on a spokes of a 12-spoke wheel, the wheel would balance on its centre.
- cardinality
- Fancy way of saying "the number of things" in a group or set. Cardinal numbers are numbers used for counting, in contrast to ordinal numbers for denoting sequence, or nominal numbers that names or identifies something. If a scale has seven tones, then its cardinality is seven.
- chiral
- The quality of being different from ones own mirror-image, in a way that can not be achieved by rotation.
- cohemitonic
- Cohemitonic scales contain two or more semitones (making them hemitonic) such that two or more of the semitones appear consecutively in scale order. Example: the Hungarian minor scale
- coherence
- An unabiguous relationship between specific intervals and generic intervals. Also known as propriety.
- complement relation
- Having all the tones that are absent from another set
- dicohemitonic
- A scale that contains exactly two semitones consecutively in scale order
- dihemitonic
- A scale that contains exactly two semitones
- distribution spectra
- The collection of the spectrum of distribution of specific intervals for each generic interval of a scale
- enantiomorph
- The result of a transformation by reflection, i.e. with its interval pattern reversed, but specifically in the case of chiral scales.
- generic interval
- The number of scale steps between two tones
- heliotonic
- A scale which can be rendered with one notehead on each line and space, using nothing more than single or double alterations
- hemitonic
- A scale that has tones separated by one semitone
- heptatonic
- A scale with seven tones. For example, the major scale is heptatonic.
- imperfection
- A scale member where the perfect fifth above it is not in the scale
- interval of equivalence
- The interval at which the pitch class is considered equivalent. In TET, the interval of equivalence is 12, aka an octave.
- interval pattern
- The sequence of semitones, tones, and larger intervals, that describe a scale. For example, a major scale is "T T S T T T S". Expressed numerically, a major scale has the interval pattern [2,2,1,2,2,2]; the final interval is implied.
- interval spectrum
- A signature invented by Howard Hanson, describing all the intervals that can be found in a sonority
- mutation
- The alteration of a scale by addition or removal of a tone, or by shifting a tone up or down by a semitone.
- normal form
- the most compact way to arrange of pitches in a set, without altering the set by transposition
- octatonic
- A scale with eight tones.
- palindromic
- A scale that has the same interval pattern forward and backward.
- pentatonic
- A scale with five tones
- pitch class set
- An unordered set of pitches, usually described in integer form.
- prime form
- The most exemplary form of a pitch class set, being the transformation that is most condensed and left-packed.
- propriety
- An unabiguous relationship between specific intervals and generic intervals. Also known as coherence.
- proximity
- The number of transformations required to change one scale into another
- ridge tone
- A pitch that appears in every scale built upon the scale degrees of itself.
- root
- The lowest tone of the scale, signifying the tone upon which all others are measured as an interval above
- scale
- A set of tones starting on a root, contained within one octave, having no more than a major third leap
- sonority
- The whole of a sound, comprised of all component tones
- specific interval
- The number of semitones between two tones
- spectra variation
- The average of the spectra widths with respect to the number of tones in a scale.
- spectrum width
- The difference between the lowest and highest specific intervals for a given generic interval.
- subset relation
- Consisting of tones that are all present within another set
- symmetry
- Having the ability to transform into itself by reflection or rotation
- tone
- A single entity having a pitch, as in one member of a scale
- trihemitonic
- A scale that contains exactly three semitones
- tritonic
- Containing one or more tritones
- truncation
- A scale produced by removing tones from another scale
- unhemitonic
- A scale that contains only one semitone
- z-relation
- The relation between two pitch class sets that have the same interval vector, but are not transpositions or inversions of each other.
This scale analysis was created by Ian Ring, Canadian Composer of works for Piano, and total music theory nerd. Scale notation generated by VexFlow, and MIDI playback by MIDI.js. Some scale names used on this and other pages are ©2005 William Zeitler (http://allthescales.org).
Pitch spelling algorithm employed here is adapted from a method by Uzay Bora, Baris Tekin Tezel, and Alper Vahaplar. (An algorithm for spelling the pitches of any musical scale) Contact authors Patent owner: Dokuz Eylül University, Used with Permission. Contact TTO
References
- [1] http://allthescales.org/
- [2] Allan Forte, The Structure of Atonal Music (1973, ISBN 0-300-02120-8).
- [3] "The Integer Model Of Pitch", Basic Atonal Theory, John Rahn p.35 ISBN 0-02-873-160-3
- [4] Howard Hanson, "Harmonic Materials Of Modern Music", ISBN 978-0891972075
- [5] Paul Nelson, "Pitch Class Sets" http://composertools.com/Theory/PCSets.pdf
- [6] http://andrewduncan.net/cmt/
- [7] Circular Distributions and Spectra Variations in Music. http://archive.bridgesmathart.org/2005/bridges2005-255.pdf
- [8] Rappoport, David. "Maximal Area Sets and Harmony". Graphs and Combinatorics, Vol 23, 2007-06-01.
- [9] Zeitler, William, table of imperfections counted in scales. https://allthescales.org/intro.html#Perfection